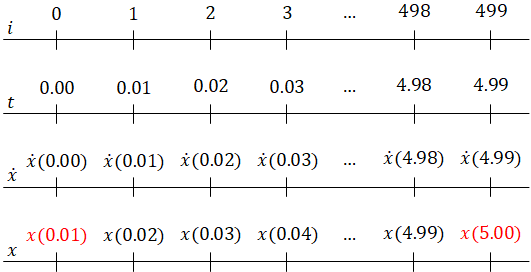Equations for state space model, or state variable model, is shown. How to choose state variables is explained with examples. Algorithm for simulation is then provided.
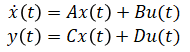
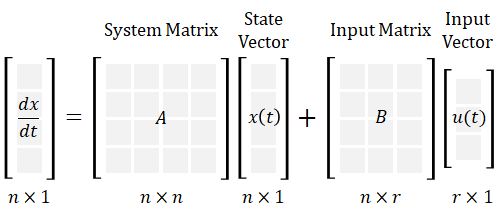
| x(t) | = | state vector | |
| u(t) | = | input vector | |
| y(t) | = | output vector | |
| A | = | system matrix (physics of system) | |
| B | = | input matrix (actuators) | |
| C | = | output matrix (sensors) | |
| D | = | maps input to output |
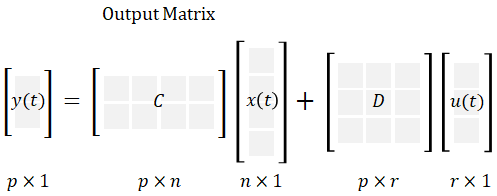
There are infinitely many ways to choose state variables for the same system but the model becomes easier to interpret if state variables represent physically identifiable variables. Below are state variables commonly chosen for each type of device.
| damper, friction | velocity |
| spring | displacement |
| mass | position, velocity |
| capacitor | voltage across capacitor |
| inductor | current through inductor |
The state variables are picked such that those variables along with the input variables are just enough to determine any future output values.
x = x0
dt = 0.01
for i = 0 ... 499
t = i * dt
xdot = A * x + B * u(t) // xdot(t) = Ax(t) + Bu(t)
x = x + xdot * dt // x(t+dt) = x(t) + xdot(t)Value after loop i: