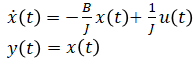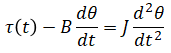
Transfer function and state space model are developed for torque applied on a mass with friction.
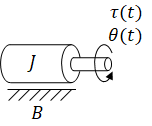
| (input) | τ(t) | = | applied torque | |
| (output) | θ(t) | = | rotation angle | unknown |
| J | = | inertia | ||
| B | = | friction coefficient |
1 unknown so 1 equation is needed.
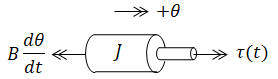
Newton's 2nd law:
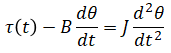
Laplace transform (eq. 1):
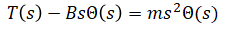
Find output/input:
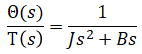
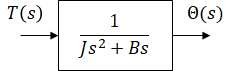
When a mass is present in a system, its position and velocity are commonly chosen as state variables. Similarly for the rotational case, angle and angular velocity are chosen for state variables. It can also be noted that applied torque (input), angle, and angular velocity are sufficient to determine this system's future angle (output). This confirms the selected state variables are valid for this system.
State vector:

Input vector:

Output vector:
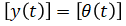
Rewrite (eq. 1) in these new notations:
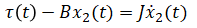
Rearrange equations to express ẋ(t) and y(t) in terms of x(t) and u(t):

Rearrange in matrix format:
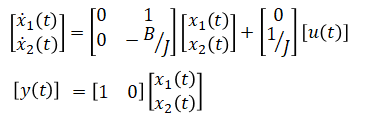
If the output is angular velocity, choosing angular velocity as the only state variable is sufficient to describe this system. This is useful for example when the motor's speed is of concern instead of its position.
State vector:
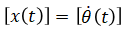
Input vector:

Output vector:
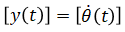
Rewrite (eq. 1) in these new notations:
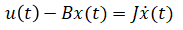
Rearrange in space state model format: