ZYX Euler angles are a common convention used in aerospace engineering to describe orientations in 3D. This page explains what ZYX Euler angles are, how to obtain rotation matrices, how to recover Euler angles from rotation matrices, and some things to be careful when dealing with them. The concepts on this page can be applied to any Euler angles. Example code is provided in Python.
Z-Y-X intrinsic rotation Euler angles are defined as follows:
This is the same as X-Y-Z extrinsic rotation:
It is one of six Tait-Bryan angles because the angles represent rotations about three distinct axes.
This is intrinsic rotation so the rotation matrices are post-multiplied:
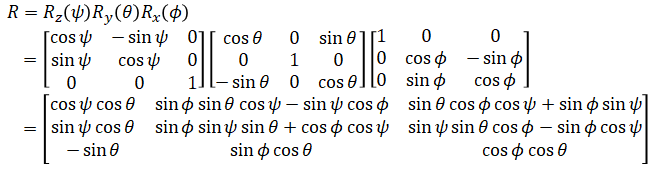
Note that some literature define elemental rotations as the transpose of how it is defined here and compose them by pre-multiplying them intead. This results in the transpose of R:
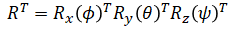
From the rotation matrix it can be seen that R31 = -sinθ so θ can be solved by:
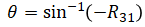
There are caveats in using arcsine which is discussed later. We also know that R11 = cosψ⋅cosθ and R21 = sinψ⋅cosθ so
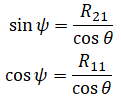
Instead of directly solving for ψ using arcsine or arccosine, we use the four-quadrant inverse tangent, atan2(y,x):
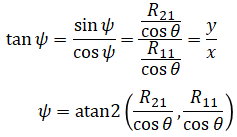
The benefit of using atan2() is discussed later. The reader may be tempted to cancel out cosθ by doing,
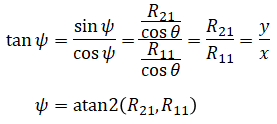
but this should not be done because
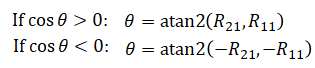
which are different.
Similarly, we know that R32 = sinφ⋅cosθ and R33 = cosφ⋅cosθ so
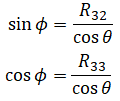
Again we use atan2(y,x) to solve for φ:
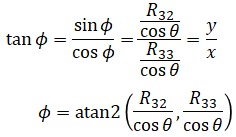
Note that for example

so if R31 = -0.5, θ can be either π/6 (30 degrees) or 5π/6 (150 degrees). asin() will pick one of the two (it picks π/6 because its range is [-π/2,π/2], or -90 to 90 degrees). But how can this be possible? Roll rotation by 30 degrees and 150 degrees are two different rotations. This is because it is possible to reach the same orientation by two different ways. For example
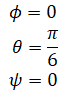
reaches the same orientation as
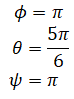
Both result in
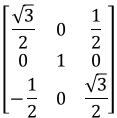
In a more general sense, the inverse of sine can be either θ or π-θ. This shows that there are two sets of Euler angles for a given rotation matrix. What is important to note is that simply using asin() will always pick θ in the range [-π/2,π/2] which is only one of the two solutions.
If cosθ = 0, then there is division by zero when calculating φ or ψ. This happens when θ = π/2 or -π/2 (roll is 90 or -90 degrees), or when R31 is -1 or 1 respectively.
Below is the rotatin matrix for when θ = π/2:
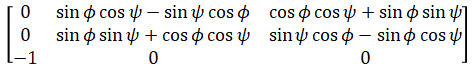
Which can be simplified using trigonometric angle sum formula as
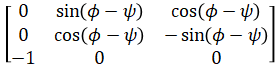
This shows that it is a function of φ-ψ. It is impossible to determine ψ without knowing φ and vise-versa. What this means is that when the orientation is such that the pitch angle is 90 degrees, there isn't a unique roll-yaw combination. At such orientations, it is possible to determine roll when yaw is known (or vise-versa) but not both at the same time.
This type of problem occurs with any Euler angles and is called a singularity. At singularities, there are infinite set of Euler angles. To illustrate the point I picked three sets of Euler angles:
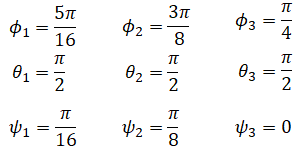
All three of the above result in the same rotation matrix:
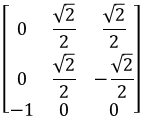
A solution is to just pick an arbitrary angle for roll or yaw (such as 0) and calculate the other.
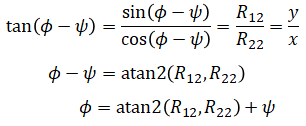
or
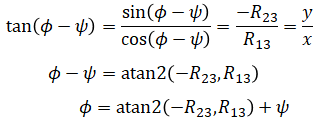
We can do the same for θ = -π/2 case. The rotatioin matrix is:
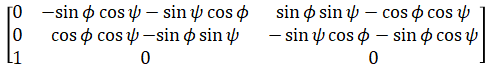
Which can be simplified using trigonometric angle sum formula as
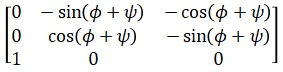
Again using R12 and R22, the relationship between φ and ψ can be calculated:
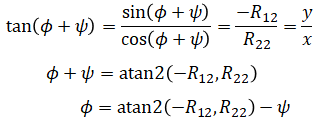
or using R23 and R13:
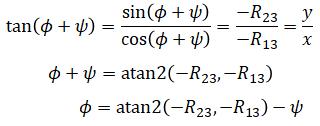
In our calculation of φ and ψ, we used atan2() instead of arcsine or arccosine (or arctangent). This is because we want to avoid ambiguities that arise when using the others.
Arcsine returns a value between [-π/2, π/2]. This is just half the circle. As mentioned previously, sin(π-θ) = sinθ so there are two valid solutions θ and π-θ but arcsine picks only one of them.
Arccosine returns a value between [0, π]. Again this is just half the circle. cosθ = cos(-θ) so both +θ and -θ are valid but only the positive value is returned when using arccosine.
Arctangent has a range (-π/2, π/2). There are two issues. First, there is ambiguity again. For example,
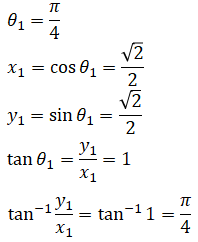
But
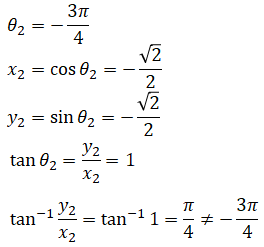
As a result, arctangent is unable to recover the angle. It fails to distinguish opposite points on the circle. The second issue is when the angle is -π/2 or π/2. It is undefined.
atan2() has a range (−π, π] which is the full circle. It avoids the ambiguities that arise from the other inverse trigonometric functions. The previous example is solved correctly:

In addition, it works at -π/2 and π/2:
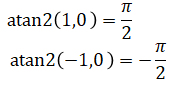
Below is an example code written in Python. scipy is used as a helper library to check whether the calculations are correct.
The rotation matrix to euler function returns two different solutions in the non-degenerate case. For the degenerate case, there are infinite solutions so the user can specify ψ (yaw). If yaw is not specified, an arbitrary value of 0 is selected by default. There is also an eps argument. Mathematically, the correct value for eps is 0 (meaning that the singular case happens only when R31 is exactly +/- 1); however, in reality, a rotation that is close to singularity already exhibits singular-like behavior (this can be observed by setting eps to 0 and seeing which test-cases fail).
from math import sin, cos, asin, atan2, pi import numpy as np from scipy.spatial.transform import Rotation import itertools def get_rotation_matrix(phi, theta, psi): sinphi = sin(phi) sintheta = sin(theta) sinpsi = sin(psi) cosphi = cos(phi) costheta = cos(theta) cospsi = cos(psi) return np.array([ [cospsi*costheta, sinphi*sintheta*cospsi-sinpsi*cosphi, sinphi*sinpsi+sintheta*cosphi*cospsi], [sinpsi*costheta, sinphi*sinpsi*sintheta+cosphi*cospsi, -sinphi*cospsi+sinpsi*sintheta*cosphi], [-sintheta, sinphi*costheta, cosphi*costheta] ]) # psi is used for singular case because there are infinite solutions # eps is used as a threshold for singular case def get_euler(R, psi=0, eps=1e-3): if -R[2,0] >= 1.0 - eps: # Singularity 1 R31 = -1 theta = pi/2 phi = atan2(R[0,1], R[1,1]) + psi phi2 = phi theta2 = theta psi2 = psi elif -R[2,0] <= -1.0 + eps: # Singularity 2 R32 = -1 theta = -pi/2 phi = atan2(-R[0,1], R[1,1]) - psi phi2 = phi theta2 = theta psi2 = psi else: theta = asin(-R[2,0]) # Range: [-pi/2, pi/2] c = cos(theta) phi = atan2(R[2,1]/c, R[2,2]/c) # Range: (−pi, pi] psi = atan2(R[1,0]/c, R[0,0]/c) # Range: (−pi, pi] theta2 = pi - theta c2 = cos(theta2) phi2 = atan2(R[2,1]/c2, R[2,2]/c2) # Range: (−pi, pi] psi2 = atan2(R[1,0]/c2, R[0,0]/c2) # Range: (−pi, pi] return phi, theta, psi, phi2, theta2, psi2 test_eps = 1e-3 def test(phi, theta, psi, R): # Check get_rotation_matrix() R2 = get_rotation_matrix(phi, theta, psi) is_same_matrix = np.all(np.abs(R - R2) < test_eps) # Check get_euler() phi2, theta2, psi2, phi3, theta3, psi3 = get_euler(R, psi) is_same_euler_1 = np.all(np.abs(np.fmod([phi-phi2, theta-theta2, psi-psi2], 2*pi)) < test_eps) is_same_euler_2 = np.all(np.abs(np.fmod([phi-phi3, theta-theta3, psi-psi3], 2*pi)) < test_eps) is_same_euler = is_same_euler_1 or is_same_euler_2 if not is_same_matrix: print(f'Matrix mismatch: {phi}, {theta}, {psi}') print(R) if not is_same_euler: print(f'Euler mismatch: {phi}, {theta}, {psi}') print(R) print('Test all angle combinations around unit circle (including singularity)') angles = [-pi, -3*pi/4, -pi/2, -pi/4, 0, pi/4, pi/2, 3*pi/4, pi] for (phi, theta, psi) in itertools.product(angles, repeat=3): R = Rotation.from_euler('ZYX', [psi, theta, phi]) test(phi, theta, psi, R.as_matrix()) print('Test random rotations') for i in range(100): R = Rotation.random() psi, theta, phi = R.as_euler('ZYX') test(phi, theta, psi, R.as_matrix())
Let the angular velocity in the body frame be p, q, r. These are related to the derivatives of the roll, pitch, yaw angles according to:
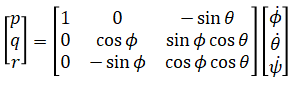
This can be derived as follows. First let the world frame be defined by fix basis {wx, wy, wz}. This is rotated by ψ around pz to make the first intermediate basis {tx, ty, tz} where pz = tz. This is again rotated about ty by θ to make the second intermediate basis {tx', ty', tz'} where ty = ty'. The final rotation happens about tx' by φ to make {bx, by, bz} where tx' = bx. This final frame is the body frame.

The basis are related by rotation matrices:
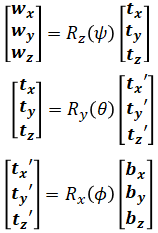
The angular velocity in the body frame is,
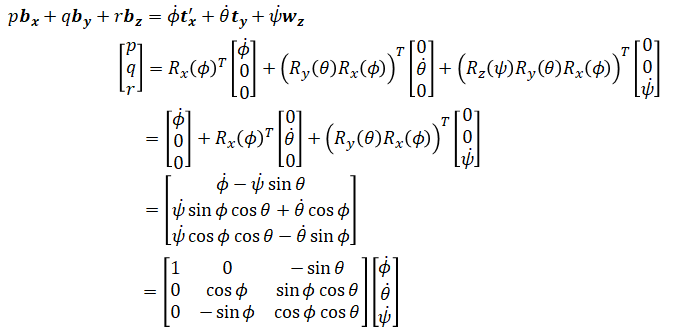
which is the result we showed at the beginning of this section.