Quaternion to Rotation Matrix

This page summarizes three different methods to convert a quaternion to a Rotation matrix. They are mathematically equivalent. Example code is provided in Python. Results are compared against those by scipy.

Let a quaternion be defined as,

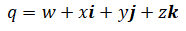
w is the scalar component and [x, y, z] is the vector component.

Method 1

Method 2

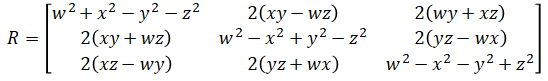
The off-diagonals are identical to those of method 1 but the diagonal elements are different. It can be shown that the diagonal elements are identical too using the fact that quaternions representing rotations are unit quaternions:

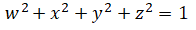
For example the first row, first column is:

Method 3

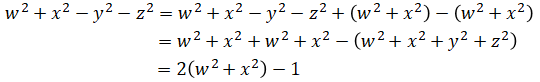
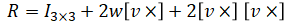
where [v×] is the skew symmetric cross product operator matrix:

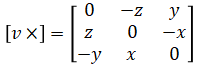
Note that the transpose can be calculated by:

Code

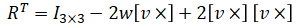
from scipy.spatial.transform import Rotation
import numpy as np

def get_rotation_matrix_1(x, y, z, w):
    w2 = w*w
    x2 = x*x
    y2 = y*y
    z2 = z*z
    r11 = w2 + x2 - y2 - z2
    r12 = 2 * (x*y - w*z)
    r13 = 2 * (w*y + x*z)
    r21 = 2 * (x*y + w*z)
    r22 = w2 - x2 + y2 - z2
    r23 = 2 * (y*z - w*x)
    r31 = 2 * (x*z - w*y)
    r32 = 2 * (y*z + w*x)
    r33 = w2 - x2 - y2 + z2
    return np.array([
        [r11, r12, r13],
        [r21, r22, r23],
        [r31, r32, r33]
    ])

def get_rotation_matrix_2(x, y, z, w):
    r11 = 2 * (w*w + x*x) - 1
    r12 = 2 * (x*y - w*z)
    r13 = 2 * (x*z + w*y)
    r21 = 2 * (x*y + w*z)
    r22 = 2 * (w*w + y*y) - 1
    r23 = 2 * (y*z - w*x)
    r31 = 2 * (x*z - w*y)
    r32 = 2 * (y*z + w*x)
    r33 = 2 * (w*w + z*z) - 1
    return np.array([
        [r11, r12, r13],
        [r21, r22, r23],
        [r31, r32, r33]
    ])

def get_rotation_matrix_3(x, y, z, w):
    c = np.array([
        [0, -z, y],
        [z, 0, -x],
        [-y, x, 0]
    ])
    return np.eye(3) + 2*w*c + 2*c@c

# Quaternion
x = 0
y = 0
z = np.sin(np.pi/4)
w = np.cos(np.pi/4)

print(Rotation.from_quat((x, y, z, w)).as_matrix())
print(get_rotation_matrix_1(x, y, z, w))
print(get_rotation_matrix_2(x, y, z, w))
print(get_rotation_matrix_3(x, y, z, w))

Output:

[[ 0. -1.  0.]
 [ 1.  0.  0.]
 [ 0.  0.  1.]]
[[ 0. -1.  0.]
 [ 1.  0.  0.]
 [ 0.  0.  1.]]
[[ 2.22044605e-16 -1.00000000e+00  0.00000000e+00]
 [ 1.00000000e+00  2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  1.00000000e+00]]
[[-2.22044605e-16 -1.00000000e+00  0.00000000e+00]
 [ 1.00000000e+00 -2.22044605e-16  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  1.00000000e+00]]

It shows that the three methods are identical and match with the result of scipy.