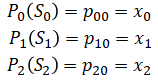
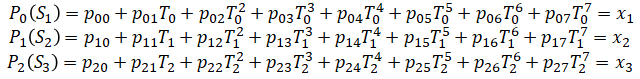
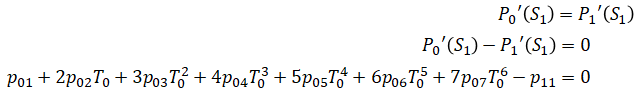 Similarly,
Similarly,

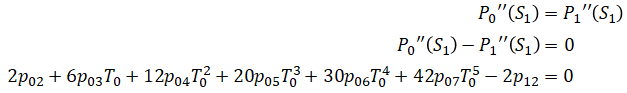 Similarly,
Similarly,
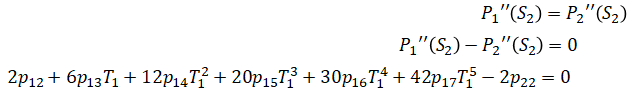
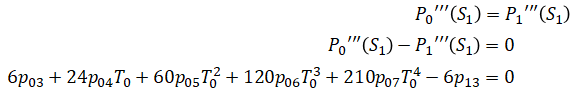 Similarly,
Similarly,
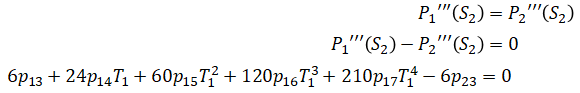
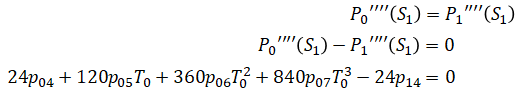 Similarly,
Similarly,
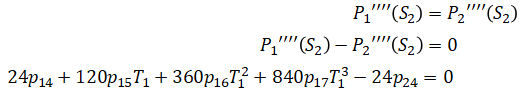
This page describes a method to generate polynomial trajectories by solving a Quadratic Programming (QP) problem. Concepts are explained through two examples. The frist example shows how to generate a minimum acceleration trajectory that passes through two points. The second example shows how to generate a minimum snap trajectory that passes through several waypoints. Python code is provided.
The first example is to find a trajectory with minimum acceleration that moves from x0=1 to xf=2 in T=10 seconds. The minimum degree of a polynomial to ensure smoothness for a minimum acceleration (2nd derivative) trajectory is 3 (i.e. cubic polynomial):
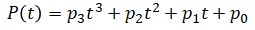
The goal is to find the four coefficients p0 to p3. To do so, we rephrase the problem as a QP problem of the form:
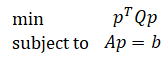
where p is the vector of the polynomial coefficients:
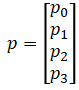
Once we rephrase it, the problem can be solved efficiently with readily available QP libraries.
Since we want to minimize the acceleration, the cost function can be written as:
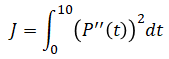
The derivatives of P(t) can be calculated as,
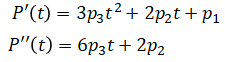
Substituting this into the cost function yields:
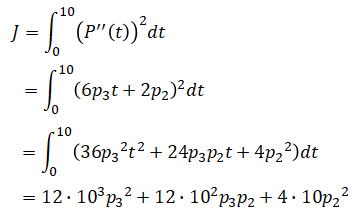
The Q matrix is found by taking the hessian matrix of J:
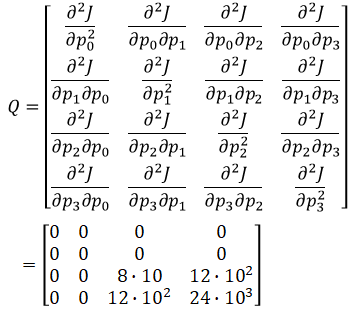
Next are the constraints:
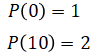
which is equivalent to,
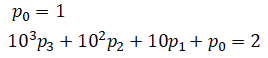
This can be rewritten in matrix form as:
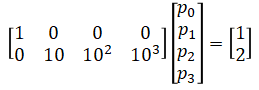
So the A matrix and b vector are given by:
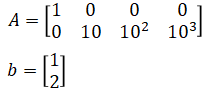
Below is a Python script to solve the QP for the above example:
import numpy as np from cvxopt import matrix, solvers x0 = 1.0 xf = 2.0 T = 10.0 Q = np.array([ [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 8*T, 12*(T**2)], [0, 0, 12*(T**2), 24*(T**3)], ]) f = np.zeros(4) A = np.array([ [1, 0, 0, 0], [1, T, T**2, T**3] ]) b = np.array([x0, xf]) sol = solvers.qp(matrix(Q), matrix(f), None, None, matrix(A), matrix(b)) print(sol['x'])
The resulting polynomial is:
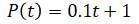
which is a line (zero acceleration) that passes through P(0)=1 and P(10)=2.
The next example is to generate a minimum snap (4th derivative) trajectory that passes through 4 waypoints at the following times:
| i | t | x |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 10 | 5 |
| 2 | 30 | 5 |
| 3 | 40 | 3 |
Since there are 4 waypoints, it is going to be a piecewise polynomial function of 3 parts. Each polynomial joins two consecutive waypoints. We will use a septic polynomial (7th degree polynomial) for each segment because that is the minimum degree required to satisfy the minimum snap requirement. Polynomial Pi(t) joins waypoints i and i+1:
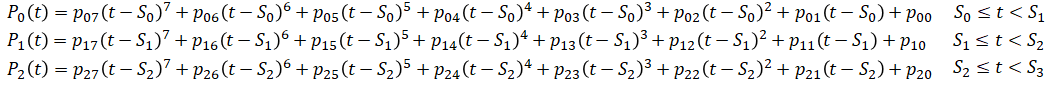
where Si are the times at the beginning of each trajectory:
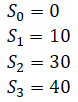
There are 3*8=24 unknown coefficients. Again the problem is set up as a QP problem:
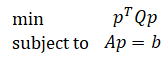
Where p is a vector of all 24 coefficients:

The Q matrix will be a 24x24 matrix. It is a block diagonal matrix made of three parts (one for each polynomial).
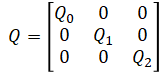
Each submatrix can be calculated this time using symbolic math:
import sympy t, T = sympy.symbols('t T') p0, p1, p2, p3, p4, p5, p6, p7 = sympy.symbols('p0 p1 p2 p3 p4 p5 p6 p7') P = p7*t**7 + p6*t**6 + p5*t**5 + p4*t**4 + p3*t**3 + p2*t**2 + p1*t + p0 P1 = sympy.diff(P, t) # Speed P2 = sympy.diff(P1, t) # Acceleration P3 = sympy.diff(P2, t) # Jerk P4 = sympy.diff(P3, t) # Snap J = sympy.integrate(P4**2, (t, 0, T)) Q = sympy.hessian(J, (p0, p1, p2, p3, p4, p5, p6, p7)) sympy.pprint(Q)
This results in:

where Ti is the time interval between waypoints i and i+1:
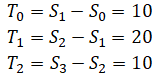
Next are the constraints (Ap=b). We will apply 14 constraints in total. A is 14x24 matrix where each row is a constraint.
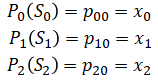
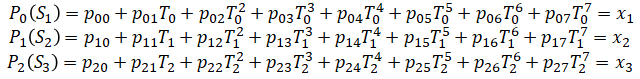
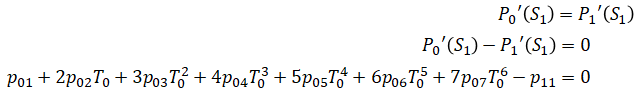 Similarly,
Similarly,

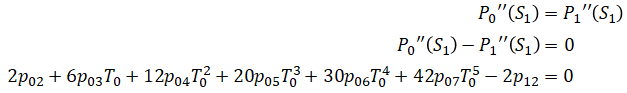 Similarly,
Similarly,
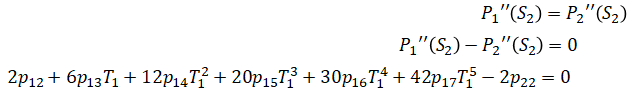
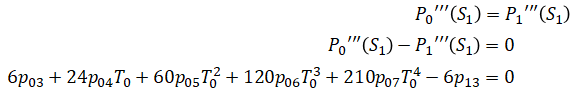 Similarly,
Similarly,
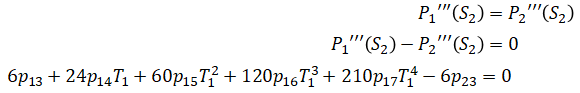
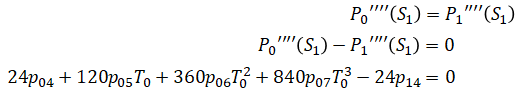 Similarly,
Similarly,
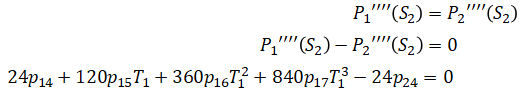
Putting all of this together in matrix form Ap = b:

Solving the QP:
import numpy as np from cvxopt import matrix, solvers import matplotlib.pyplot as plt def get_Q(T): return np.array([ [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1152*T, 2880*T**2, 5760*T**3, 10080*T**4], [0, 0, 0, 0, 2880*T**2, 9600*T**3, 21600*T**4, 40320*T**5], [0, 0, 0, 0, 5760*T**3, 21600*T**4, 51840*T**5, 100800*T**6], [0, 0, 0, 0, 10080*T**4, 40320*T**5, 100800*T**6, 201600*T**7] ]) def get_coefficients(T, wp): N = 8 # Septic polynomial has 8 coefficients M = len(T) # Number of polynomial segments L = 14 # Number of constraints # Q Matrix Z = np.zeros((N, N)) Q0 = get_Q(T[0]) Q1 = get_Q(T[1]) Q2 = get_Q(T[2]) Q = np.block([ [Q0, Z, Z], [Z, Q1, Z], [Z, Z, Q2] ]) f = np.zeros(N*M) # Constraints (Ap=b) A = np.zeros((L, N*M)) # Start position of polynomials A[0,:8] = [1, 0, 0, 0, 0, 0, 0, 0] A[1,8:16] = [1, 0, 0, 0, 0, 0, 0, 0] A[2,16:] = [1, 0, 0, 0, 0, 0, 0, 0] # End position of polynomials A[3,:8] = [1, T[0], T[0]**2, T[0]**3, T[0]**4, T[0]**5, T[0]**6, T[0]**7] A[4,8:16] = [1, T[1], T[1]**2, T[1]**3, T[1]**4, T[1]**5, T[1]**6, T[1]**7] A[5,16:] = [1, T[2], T[2]**2, T[2]**3, T[2]**4, T[2]**5, T[2]**6, T[2]**7] # Continuous velocity A[6,:16] = [0, 1, 2*T[0], 3*T[0]**2, 4*T[0]**3, 5*T[0]**4, 6*T[0]**5, 7*T[0]**6, 0, -1, 0, 0, 0, 0, 0, 0] A[7,8:] = [0, 1, 2*T[1], 3*T[1]**2, 4*T[1]**3, 5*T[1]**4, 6*T[1]**5, 7*T[1]**6, 0, -1, 0, 0, 0, 0, 0, 0] # Continuous acceleration A[8,:16] = [0, 0, 2, 6*T[0], 12*T[0]**2, 20*T[0]**3, 30*T[0]**4, 42*T[0]**5, 0, 0, -2, 0, 0, 0, 0, 0] A[9,8:] = [0, 0, 2, 6*T[1], 12*T[1]**2, 20*T[1]**3, 30*T[1]**4, 42*T[1]**5, 0, 0, -2, 0, 0, 0, 0, 0] # Continuous jerk A[10,:16] = [0, 0, 0, 6, 24*T[0], 60*T[0]**2, 120*T[0]**3, 210*T[0]**4, 0, 0, 0, -6, 0, 0, 0, 0] A[11,8:] = [0, 0, 0, 6, 24*T[1], 60*T[1]**2, 120*T[1]**3, 210*T[1]**4, 0, 0, 0, -6, 0, 0, 0, 0] # Continuous snap A[12,:16] = [0, 0, 0, 0, 24, 120*T[0], 360*T[0]**2, 840*T[0]**3, 0, 0, 0, 0, -24, 0, 0, 0] A[13,8:] = [0, 0, 0, 0, 24, 120*T[1], 360*T[1]**2, 840*T[1]**3, 0, 0, 0, 0, -24, 0, 0, 0] b = np.zeros(L) b[:6] = [wp[0], wp[1], wp[2], wp[1], wp[2], wp[3]] sol = solvers.qp(matrix(Q), matrix(f), None, None, matrix(A), matrix(b)) return list(sol['x']) # Waypoints wp_t = np.array([0., 10., 30., 40.]) wp_x = np.array([0., 5., 5., 3.]) T = np.ediff1d(wp_t) p = get_coefficients(T, wp_x) N = 500 t = np.linspace(wp_t[0], wp_t[-1], N) pos = [None] * N vel = [None] * N acc = [None] * N jrk = [None] * N snp = [None] * N for i in range(N): j = np.nonzero(t[i] <= wp_t)[0][0] - 1 j = np.max([j, 0]) ti = t[i] - wp_t[j] x_coeff = np.flip(p[8*j:8*j+8]) v_coeff = np.polyder(x_coeff) a_coeff = np.polyder(v_coeff) j_coeff = np.polyder(a_coeff) s_coeff = np.polyder(j_coeff) pos[i] = np.polyval(x_coeff, ti) vel[i] = np.polyval(v_coeff, ti) acc[i] = np.polyval(a_coeff, ti) jrk[i] = np.polyval(j_coeff, ti) snp[i] = np.polyval(s_coeff, ti) plt.subplot(5, 1, 1) plt.plot(t, pos, label='Position') plt.plot(wp_t, wp_x, '.', label='Waypoint') plt.legend() plt.subplot(5, 1, 2) plt.plot(t, vel, label='velocity') plt.legend() plt.subplot(5, 1, 3) plt.plot(t, acc, label='acceleration') plt.legend() plt.subplot(5, 1, 4) plt.plot(t, jrk, label='jerk') plt.legend() plt.subplot(5, 1, 5) plt.plot(t, snp, label='snap') plt.legend() plt.xlabel('Time') plt.show()
Output:
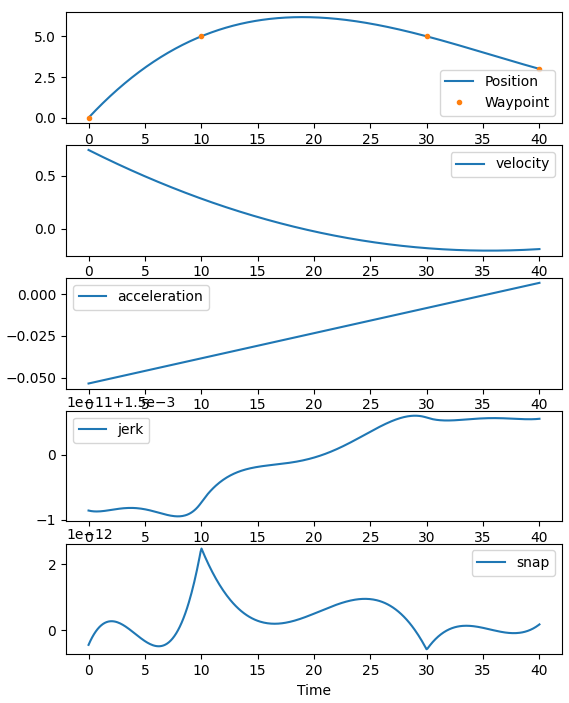
It can be seen that the trajectory passes through all the waypoints and it is continuous up to the snap.