Kalman Filter for 1D Motion

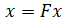
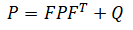
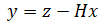
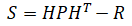
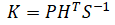
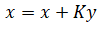
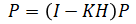
This page describes a method to estimate position and velocity in 1D given position and velocity measurements from devices like GNSS. Kalman filter with constant velocity model is used. A working Python code is also provided.

Overview

Given system and measurement equations,

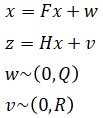
Discrete-time Kalman filter steps are,

1. Prediction: state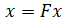
2. Prediction: covariance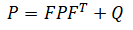
3. Innovation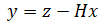
4. Innovation: covariance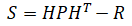
5. Kalman gain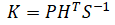
6. Update: state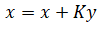
7. Update: state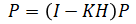

State, x

State vector is:

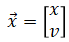
The first parameter is position (m) and the second parameter is velocity (m/sec).

State Transition Model, F

State transition matrix F is needed to predict the state and covariance. F is a 2x2 matrix given by:

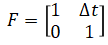
F is derived as follows:

Constant velocity model is given by,

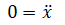
Let

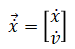
then the equation of motion in state-space form is

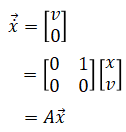
where A is the system matrix (continuous). Above can be discretized as

Process Noise, Q

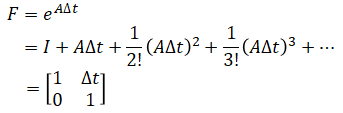
Process noise is a 2x2 matrix and is assumed to be zero:

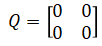
Upper left value is position variance and lower right is velocity variance.

Observation, z

There are two types of observations: position and velocity (both scalar).

Observation Model, H

Position

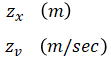
The measurement equation for position observation is,

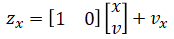
so the observation model is

Velocity

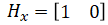
The measurement equation for velocity observation is,

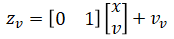
so the observation model is

Note

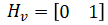
It is possible to set up measurement equation for both position and velocity observations at the same time:

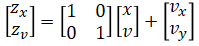
Updating the position and then the velocity separately is the same as updating them at the same time using the above equation.

Observation Noise, R

Observation noise is given by,

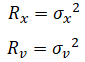
σx is 1-standard deviation position error (positional accuracy estimate) in m obtained from GNSS receiver (often called eph).

σv is 1-standard deviation speed error (speed accuracy estimate) in m/sec obtained from GNSS receiver (often called sAcc).

Python Implementation

filter.py

import numpy as np


class KF:
    def __init__(self, x0=0, v0=0, x0_acc=0.5, v0_acc=0.5):
        '''
        x0 -- initial position [m]
        v0 -- initial velocity [m/sec]
        x0_acc -- initial position accuracy (1-standard deviation) [m]
        v0_acc -- initial velocity accuracy (1-standard deviation) [m/sec]
        '''
        self.x = np.array([[x0], [v0]]) # State
        self.P = np.diag([x0_acc ** 2, v0_acc ** 2]) # Covariance
        self.Q = np.zeros((2, 2)) # Process noise
    
    def predict(self, dt):
        '''
        dt -- time step [sec]
        '''
        F = np.array([
            [1, dt],
            [0,  1]
        ])
        self.x = F @ self.x
        self.P = F @ self.P @ F.T + self.Q
    
    def update(self, z, H, R):
        y = z - H @ self.x
        S = H @ self.P @ H.T + R
        K = (self.P @ H.T) @ np.linalg.inv(S)
        self.x = self.x + K @ y
        self.P = (np.identity(2) - K @ H) @ self.P

    def update_pos(self, pos, pos_acc):
        '''
        pos -- position measurement [m]
        pos_acc -- position measurement accuracy (1-standard deviation) [m]
        '''
        z = np.array([[pos]])
        H = np.array([
            [1, 0]
        ])
        R = np.array([[pos_acc ** 2]])
        self.update(z, H, R)

    def update_vel(self, vel, vel_acc):
        '''
        vel -- velocity measurement [m/sec]
        vel_acc -- velocity measurement accuracy (1-standard deviation) [m/sec]
        '''
        z = np.array([[vel]])
        H = np.array([
            [0, 1]
        ])
        R = np.array([[vel_acc ** 2]])
        self.update(z, H, R)

Simulation Test

True vs estimated values are compared using simulated sensor data.

Test 1: stationary

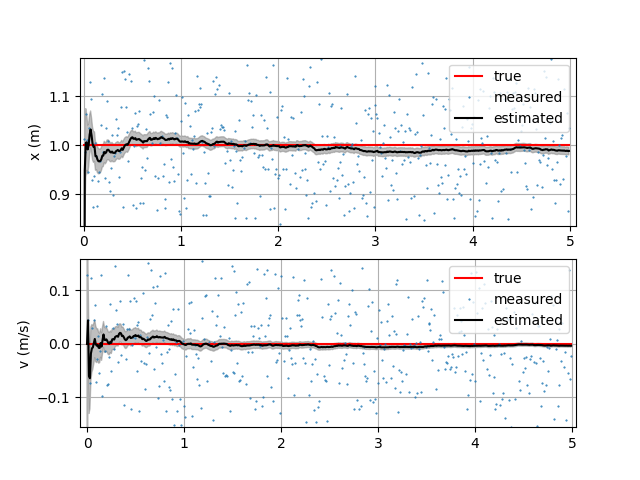
Target is not moving and is fixed at x=1m position. Position error starts large, decreases, and converges to a value. Velocity error keeps decreassing due to zero process noise.

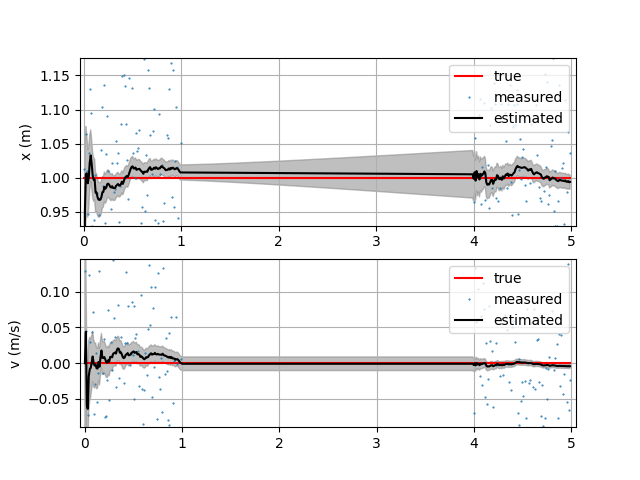
Test 2: stationary with measurement loss

Target is not moving and there is no measurement between 1 to 4 seconds. This is the case when GNSS is temporarily unavailable due to environmnetal factors. Position error increases while there is no measurement. Velocity error is constant (due to zero process noise) while there is no measurement. Velocity error diminishes once data is available.

Test 3: moving at constant velocity

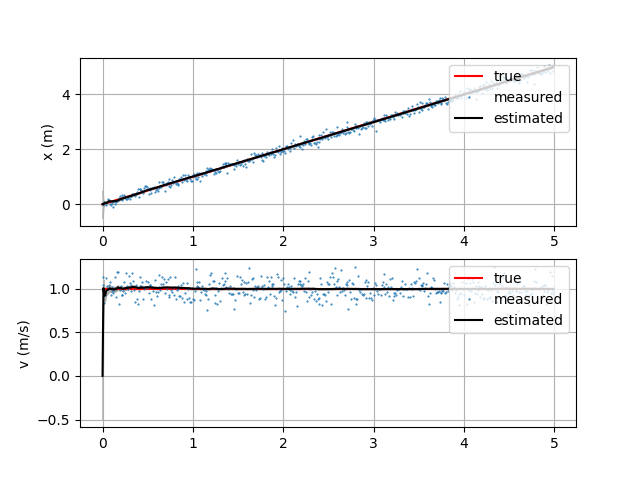
Target moves at a constant speed of 1m/sec. There is no problem tracking.

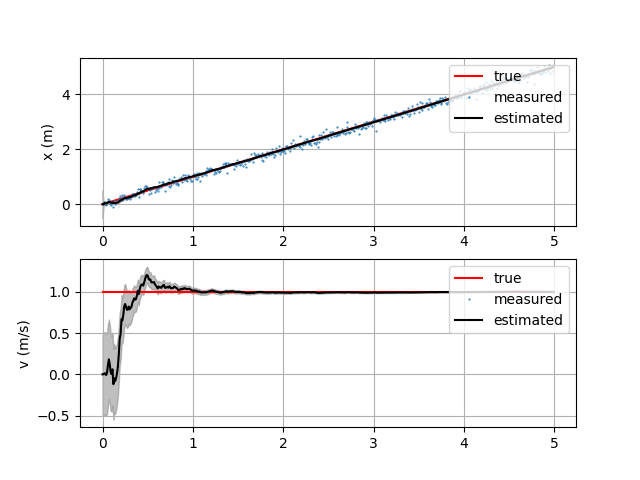
Test 4: moving at constant velocity with only position measurements

Target moves at a constant speed of 1m/sec. Only position measurements are supplied. This is the case, for example when using motion capture system (velocity information is not available). Kalman filter is able to recover velocity correctly.

Test 5: moving in sine wave

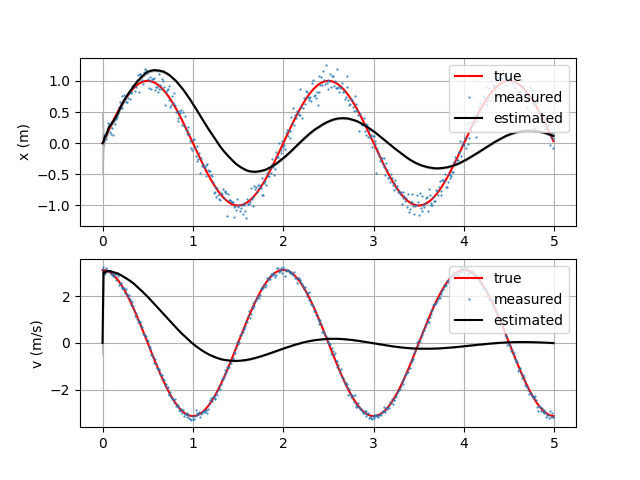
Target moves in a sine wave of 0.5Hz with 1m amplitude. Tracking fails because we are using a constant velocity model with zero process noise. A solution is to use a different model or use non-zero process noise.

Source code for the above tests

It is assumed that filter.py is placed in the same folder as the below script.

import matplotlib.pyplot as plt
import numpy as np
import filter


random_generator = np.random.default_rng(0)


def plot(t, ground_truth, gnss, estimated):
    estimated_x = np.array(estimated['x'])
    estimated_v = np.array(estimated['v'])
    x_std = np.array(estimated['x_std'])
    v_std = np.array(estimated['v_std'])

    fig, axs = plt.subplots(2, 1)

    axs[0].plot(t, ground_truth['x'], color='red', label='true')
    axs[0].plot(t, gnss['x'], '.', markersize=1, label='measured')
    axs[0].plot(t, estimated_x, color='black', label='estimated')
    axs[0].fill_between(t, 
                        estimated_x-x_std,
                        estimated_x+x_std,
                        color='gray', alpha=0.5)
    axs[0].grid(True)
    axs[0].legend(loc='upper right')
    axs[0].set_ylabel('x (m)')

    axs[1].plot(t, ground_truth['v'], color='red', label='true')
    axs[1].plot(t, gnss['v'], '.', markersize=1, label='measured')
    axs[1].plot(t, estimated_v, color='black', label='estimated')
    axs[1].fill_between(t, 
                        estimated_v-v_std,
                        estimated_v+v_std,
                        color='gray', alpha=0.5)
    axs[1].grid(True)
    axs[1].legend(loc='upper right')
    axs[1].set_ylabel('v (m/s)')

    plt.show()


def estimate(t, gnss):
    N = len(t)
    result = {
        'x'    : [None] * N,
        'v'    : [None] * N,
        'x_std': [None] * N,
        'v_std': [None] * N
    }
    kf = filter.KF()

    result['x'][0] = kf.x[0, 0]
    result['v'][0] = kf.x[1, 0]
    result['x_std'][0] = np.sqrt(kf.P[0, 0])
    result['v_std'][0] = np.sqrt(kf.P[1, 1])
    for i in range(1, N):
        dt = t[i] - t[i-1]
        kf.predict(dt)
        if ~np.isnan(gnss['x'][i]):
            kf.update_pos(gnss['x'][i], gnss['x_std'][i])
        if ~np.isnan(gnss['v'][i]):
            kf.update_vel(gnss['v'][i], gnss['v_std'][i])
        result['x'][i] = kf.x[0, 0]
        result['v'][i] = kf.x[1, 0]
        result['x_std'][i] = np.sqrt(kf.P[0, 0])
        result['v_std'][i] = np.sqrt(kf.P[1, 1])

    return result


def generate_test1_data():
    # Generate time
    dt = 0.01
    t = np.arange(0, 5, 0.01)

    # Generate ground truth data
    # Position stationary
    x0 = 1
    ground_truth = {}
    ground_truth['x'] = 0 * t + x0
    ground_truth['v'] = np.gradient(ground_truth['x'], t)
    ground_truth['a'] = np.gradient(ground_truth['v'], t)

    # Generate GNSS sensor data
    stdev = 0.1
    gnss = {
        'x'    : random_generator.normal(ground_truth['x'], stdev),
        'x_std': [stdev] * len(t),
        'v'    : random_generator.normal(ground_truth['v'], stdev),
        'v_std': [stdev] * len(t)
    }

    return t, ground_truth, gnss


def generate_test2_data():
    # Generate time
    dt = 0.01
    t = np.arange(0, 5, dt)

    # Generate ground truth data
    # Position stationary
    x0 = 1
    ground_truth = {}
    ground_truth['x'] = 0 * t + x0
    ground_truth['v'] = np.gradient(ground_truth['x'], t)

    # Generate GNSS sensor data
    stdev = 0.1
    gnss = {
        'x'    : random_generator.normal(ground_truth['x'], stdev),
        'x_std': [stdev] * len(t),
        'v'    : random_generator.normal(ground_truth['v'], stdev),
        'v_std': [stdev] * len(t)
    }

    # Remove GNSS data betweeen 1 to 4 seconds
    for i in range(len(t)):
        if t[i] > 1 and t[i] < 4:
            gnss['x'][i], gnss['x_std'][i] = np.nan, np.nan
            gnss['v'][i], gnss['v_std'][i] = np.nan, np.nan

    return t, ground_truth, gnss


def generate_test3_data():
    # Generate time
    dt = 0.01
    t = np.arange(0, 5, dt)

    # Generate ground truth data
    # Position moving at constant velocity
    v = 1
    ground_truth = {}
    ground_truth['x'] = v * t
    ground_truth['v'] = np.gradient(ground_truth['x'], t)

    # Generate GNSS sensor data
    stdev = 0.1
    gnss = {
        'x'    : random_generator.normal(ground_truth['x'], stdev),
        'x_std': [stdev] * len(t),
        'v'    : random_generator.normal(ground_truth['v'], stdev),
        'v_std': [stdev] * len(t)
    }

    return t, ground_truth, gnss


def generate_test4_data():
    # Generate time
    dt = 0.01
    t = np.arange(0, 5, dt)

    # Generate ground truth data
    # Position moving at constant velocity
    v = 1
    ground_truth = {}
    ground_truth['x'] = v * t
    ground_truth['v'] = np.gradient(ground_truth['x'], t)

    # Generate GNSS sensor data (only position)
    stdev = 0.1
    gnss = {
        'x'    : random_generator.normal(ground_truth['x'], stdev),
        'x_std': [stdev] * len(t),
        'v'    : [np.nan] * len(t),
        'v_std': [np.nan] * len(t)
    }

    return t, ground_truth, gnss


def generate_test5_data():
    # Generate time
    dt = 0.01
    t = np.arange(0, 5, dt)

    # Generate ground truth data
    # Position moving in sine wave
    f = 0.5
    ground_truth = {}
    ground_truth['x'] = np.sin(2 * np.pi * f * t)
    ground_truth['v'] = np.gradient(ground_truth['x'], t)

    # Generate GNSS sensor data
    stdev = 0.1
    gnss = {
        'x'    : random_generator.normal(ground_truth['x'], stdev),
        'x_std': [stdev] * len(t),
        'v'    : random_generator.normal(ground_truth['v'], stdev),
        'v_std': [stdev] * len(t)
    }

    return t, ground_truth, gnss


# Generate test data
#t, ground_truth, gnss = generate_test1_data()
#t, ground_truth, gnss = generate_test2_data()
#t, ground_truth, gnss = generate_test3_data()
#t, ground_truth, gnss = generate_test4_data()
t, ground_truth, gnss = generate_test5_data()

# Estimate with Kalman filter
estimated = estimate(t, gnss)

# Graph result
plot(t, ground_truth, gnss, estimated)