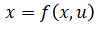
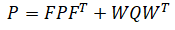
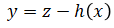
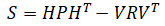
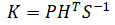
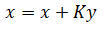
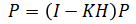
This page describes a method to estimate orientation given gyroscope and accelerometer data. Extended Kalman filter (EKF) is used with quaternion as state vector. A working Python code is also provided.
Given system and measurement equations,
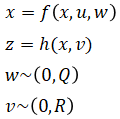
Discrete-time EKF steps are,
| 1. | Prediction: state | 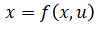 |
| 2. | Prediction: covariance | 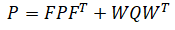 |
| 3. | Innovation | 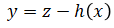 |
| 4. | Innovation: covariance | 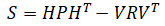 |
| 5. | Kalman gain | 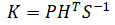 |
| 6. | Update: state | 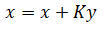 |
| 7. | Update: state | 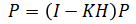 |
where
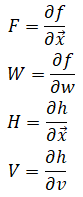
Gyroscope data are assumed to be angular velocity in rad/sec in the body frame:
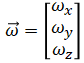
Gyroscope data are not treated as observations. Instead, they are used in the prediction step. This is done because modeling the system dynamics accurately is difficult [1].
Accelerometer data are assumed to be in m/s^2 in the body frame:
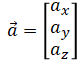
Accelerometer data are treated as observations. The device acceleration is assumed to be small enough so that the accelerometer vector always points up relative to the ground.
Front-right-down for body frame (sensor frame). NED for world frame. For example, accelerometer measures
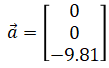
when the device is not rotated (when body frame matches world frame).
⨂ denotes quaternion multiplication defined by:
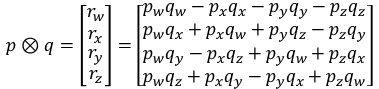
Not to be confused with some papers [2] that define the product in reverse order.
State vector is quaternion:
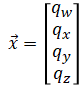
It is a unit quaternion and represents the orientation of the device. It is normalized every time it is modified. The four components of the quaternion is treated as independent parameters.
The state is modified with gyroscope data. Below are two ways to do this.
First, calculate the rotation vector for the current time step
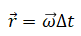
Next, convert the rotation vector to axis angle representation:
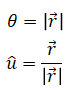
Then, convert it to quaternion:
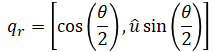
The state is predicted as follows:
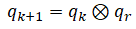
We are post-multiplying because qr is done relative to the body frame.
Use the below approximation to update the state:
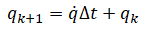
where the quaternion derivative, qdot, is given by:
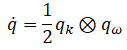
where
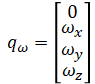
State transition matrix F is needed to predict the covariance P. F is a 4x4 matrix given by:
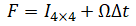
where
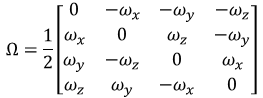
Three ways to derive F are provided:
Axis-angle representation for a rotation (θ, û) is equivalent to the unit quaternion representation:
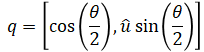
An infinitesimal rotation is then
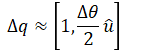
Rotation vector for the current time step is given by
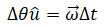
then,
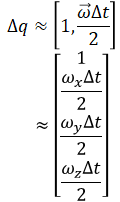
The discretized dynamics is then

The jacobian of the above is given by
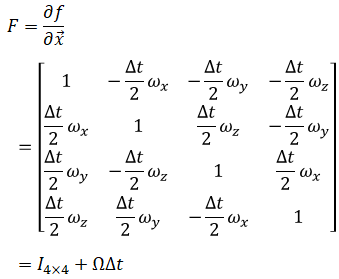
Quaternion derivative is given by
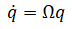
which can be discretized as
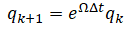
using the matrix exponential formula:
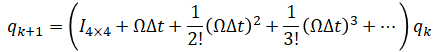
The above can be approximated by only taking the first two terms as,
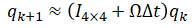
The jacobian of the above is identical to that from drivation 1.
Quaternion derivative can be approximated as
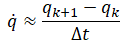
which can be rearranged as:
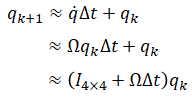
The jacobian of the above is identical to that from derivation 1 and 2.
Gyroscope noise appears as state noise and not observation noise. Process noise is given by,
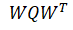
where
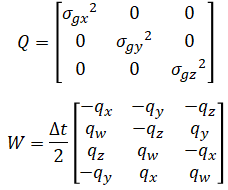
σgx, σgy, σgz are gyro noise in rad/sec.
From the previous section, we know that
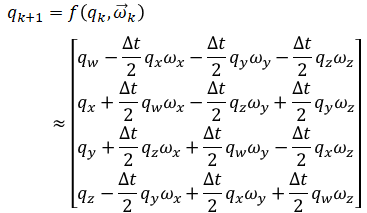
So the jacobian is:
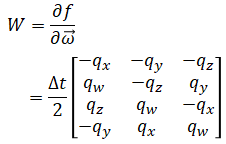
Observation vector is the gravity vector in body frame in m/s^2:
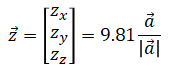
where vector a is accelerometer measurement. Only the accelerometer measurement vector direction is used.
Observation model maps the state space into the observed space:
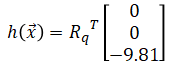
where Rq is the rotation matrix representing the orientation. The above converts the gravity vector in world frame to body frame. Quaternion to rotation matrix is given by
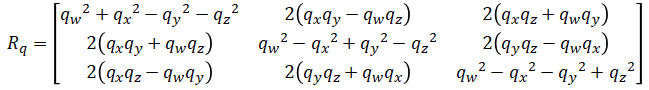
Not to be confused with some papers [2] that define the rotation matrix as the transpose of the above.
Observation matrix is determined by taking the jacobian of the observation function:
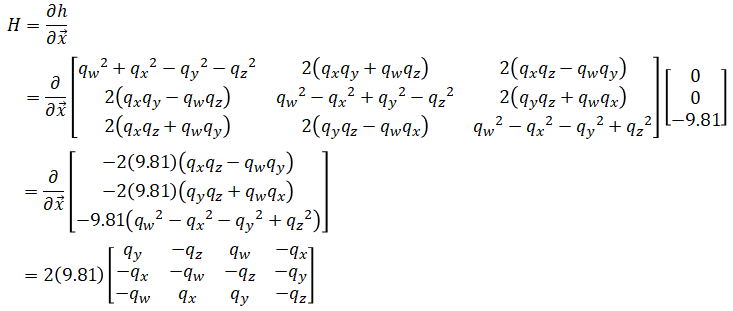
Accelerometer noise appears as observation noise. Observation noise is given by,
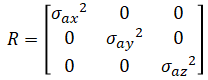
σax, σay, σaz are accelerometer noise in m/s^2
ekf.py
import numpy as np g = 9.80665 def normalize(v): return np.array(v) / np.linalg.norm(v) def quaternion_to_matrix(q): w, x, y, z = q w2 = w * w x2 = x * x y2 = y * y z2 = z * z r11 = w2 + x2 - y2 - z2 r12 = 2 * (x * y - w * z) r13 = 2 * (x * z + w * y) r21 = 2 * (x * y + w * z) r22 = w2 - x2 + y2 - z2 r23 = 2 * (y * z - w * x) r31 = 2 * (x * z - w * y) r32 = 2 * (y * z + w * x) r33 = w2 - x2 - y2 + z2 return np.array([ [r11, r12, r13], [r21, r22, r23], [r31, r32, r33] ]) def quaternion_multiply(p, q): r0 = p[0] * q[0] - p[1] * q[1] - p[2] * q[2] - p[3] * q[3] r1 = p[0] * q[1] + p[1] * q[0] + p[2] * q[3] - p[3] * q[2] r2 = p[0] * q[2] - p[1] * q[3] + p[2] * q[0] + p[3] * q[1] r3 = p[0] * q[3] + p[1] * q[2] - p[2] * q[1] + p[3] * q[0] return [r0, r1, r2, r3] def quaternion_from_axis_angle(unit_axis, angle_rad): sin_half = np.sin(angle_rad / 2) q0 = np.cos(angle_rad / 2) q1 = unit_axis[0] * sin_half q2 = unit_axis[1] * sin_half q3 = unit_axis[2] * sin_half return [q0, q1, q2, q3] def quaternion_from_rotation_vector(v, eps=0): angle_rad = np.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]) # Guard against division by zero if angle_rad > eps: unit_axis = [v[0]/angle_rad, v[1]/angle_rad, v[2]/angle_rad] q_unit = quaternion_from_axis_angle(unit_axis, angle_rad) else: q_unit = [1, 0, 0, 0] return q_unit def get_F(w, dt): wx, wy, wz = w Omega = 1/2 * np.array([ [ 0, -wx, -wy, -wz], [wx, 0, wz, -wy], [wy, -wz, 0, wx], [wz, wy, -wx, 0] ]) return np.identity(4) + Omega * dt def get_W(q, dt): qw, qx, qy, qz = q return dt/2 * np.array([ [-qx, -qy, -qz], [ qw, -qz, qy], [ qz, qw, -qx], [-qy, qx, qw] ]) def get_H(q): qw, qx, qy, qz = q return 2 * g * np.array([ [ qy, -qz, qw, -qx], [-qx, -qw, -qz, -qy], [-qw, qx, qy, -qz] ]) def f(x, w, dt): d_ang = np.array(w) * dt dq = quaternion_from_rotation_vector(d_ang) x = quaternion_multiply(x, dq) x = normalize(x) return x def h(x): R_from_body = quaternion_to_matrix(x) R_to_body = R_from_body.T return R_to_body @ np.array([[0], [0], [-g]]) class EKF: def __init__(self, q0=[1,0,0,0], gyro_noise=0.015, accelerometer_noise=1.0): ''' q0 -- initial orientation (unit quaternion) [qw, qx, qy, qz] gyro_noise -- [rad/sec] accelerometer_noise -- [m/s^2] ''' self.x = q0 self.P = np.identity(4) * 0.01 self.Q = np.identity(3) * (gyro_noise ** 2) self.R = np.identity(3) * (accelerometer_noise ** 2) def predict(self, w, dt): ''' w -- gyro measurement in front-right-down coordinates [rad/sec] dt -- time step [sec] ''' F = get_F(w, dt) W = get_W(self.x, dt) self.x = f(self.x, w, dt) self.P = F @ self.P @ F.T + W @ self.Q @ W.T def update(self, a): ''' a -- accelerometer measurement in front-right-down coordinates [m/s^2] ''' a = np.array(a).reshape(3, 1) z = g * normalize(a) y = z - h(self.x) H = get_H(self.x) S = H @ self.P @ H.T + self.R K = (self.P @ H.T) @ np.linalg.inv(S) self.x = self.x + (K @ y)[:,0] self.x = normalize(self.x) self.P = (np.identity(4) - K @ H) @ self.P
True vs estimated attitudes are compared using simulated sensor data. Euler angles are z-y-x intrinsic Tait-Bryan rotation (e.g. first rotate about Z-axis by angle yaw, next rotate about the newly created Y-axis by angle pitch, finally rotate about the newly created X-axis by angle roll).
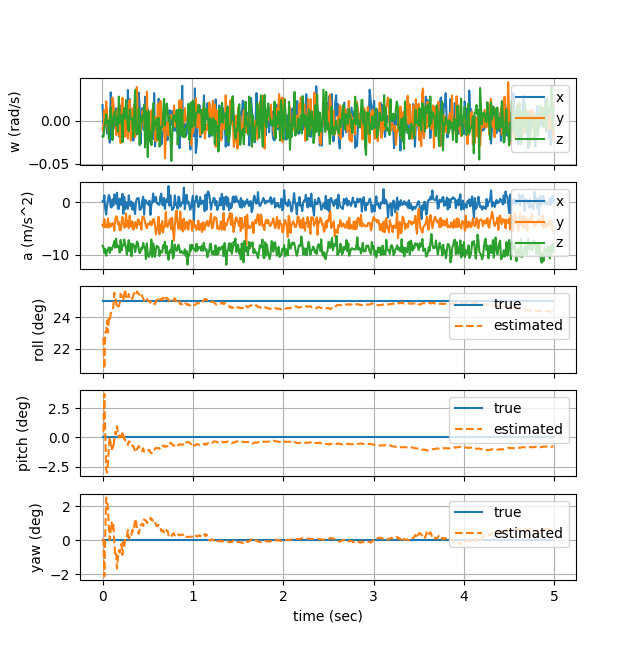
IMU is held fixed (non-rotating) at roll 25 degrees, pitch 0 degrees, yaw 0 degrees. Since the initial orientation is roll 0 degrees, pitch 0 degrees, yaw 0 degrees, it takes about 1 second for the estimate to stabilize to the true value.
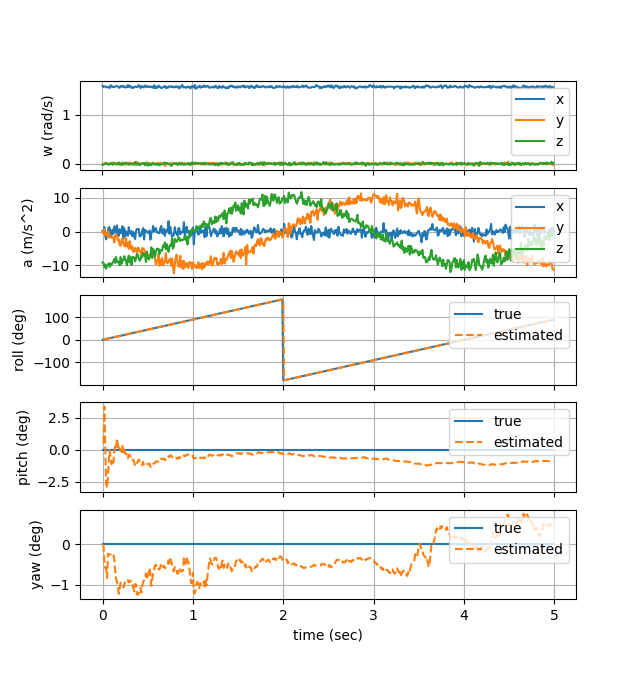
IMU is rotated around the x-axis at constant angular rate of 90 degrees/sec. It can be seen that the roll is estimated correctly even after going full rotation. Pitch and yaw (which are kept constant) is accurate to about +/-1 degree. Pitch is inaccurate to about 2.5 degrees at the beginning most likely because the state covariance has not reached steady state yet.
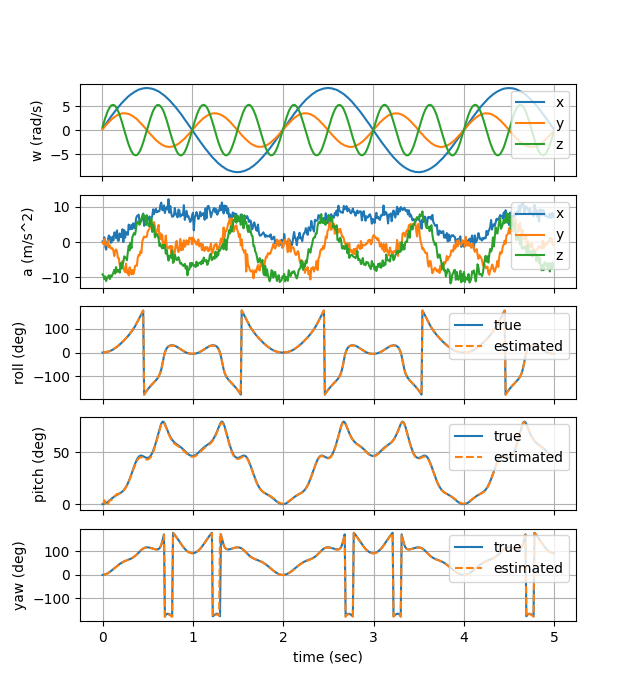
IMU is rotated all axes at the same time. It can be seen that the estimated orientation closely matches the true value.
It is assumed that ekf.py is placed in the same folder as the below script.
import matplotlib.pyplot as plt import numpy as np from ekf import EKF from ekf import quaternion_multiply from ekf import quaternion_from_axis_angle from ekf import normalize from ekf import g random_generator = np.random.default_rng(0) def quaternion_identity(): return [1, 0, 0, 0] def quaternion_inv(q_unit): return [q_unit[0], -q_unit[1], -q_unit[2], -q_unit[3]] def rotate_vector(q_unit, v): p = [0.0, v[0], v[1], v[2]] # q * p * q^-1 r = quaternion_multiply( quaternion_multiply(q_unit, p), quaternion_inv(q_unit)) return [r[1], r[2], r[3]] def quaternion_to_euler(q): roll = np.arctan2(2 * (q[0] * q[1] + q[2] * q[3]), 1 - 2 * (q[1] * q[1] + q[2] * q[2])) pitch = np.arcsin(2 * (q[0] * q[2] - q[3] * q[1])) yaw = np.arctan2(2 * (q[0] * q[3] + q[1] * q[2]), 1 - 2 * (q[2] * q[2] + q[3] * q[3])) return roll, pitch, yaw def quaternion_from_euler(roll, pitch, yaw): c_roll = np.cos(roll / 2) s_roll = np.sin(roll / 2) c_pitch = np.cos(pitch / 2) s_pitch = np.sin(pitch / 2) c_yaw = np.cos(yaw / 2) s_yaw = np.sin(yaw / 2) q0 = c_roll * c_pitch * c_yaw + s_roll * s_pitch * s_yaw q1 = s_roll * c_pitch * c_yaw - c_roll * s_pitch * s_yaw q2 = c_roll * s_pitch * c_yaw + s_roll * c_pitch * s_yaw q3 = c_roll * c_pitch * s_yaw - s_roll * s_pitch * c_yaw return [q0, q1, q2, q3] def plot(ts, w, a, rpy, estimated_rpy): fig, axs = plt.subplots(5, 1) axs[0].plot(ts, w[0], label='x') axs[0].plot(ts, w[1], label='y') axs[0].plot(ts, w[2], label='z') axs[0].grid(True) axs[0].legend(loc='upper right') axs[0].set_ylabel('w (rad/s)') axs[0].set_xticklabels([]) axs[1].plot(ts, a[0], label='x') axs[1].plot(ts, a[1], label='y') axs[1].plot(ts, a[2], label='z') axs[1].grid(True) axs[1].legend(loc='upper right') axs[1].set_ylabel('a (m/s^2)') axs[1].set_xticklabels([]) axs[2].plot(ts, rpy[0], label='true') axs[2].plot(ts, estimated_rpy[0], '--', label=f'estimated') axs[2].grid(True) axs[2].legend(loc='upper right') axs[2].set_ylabel('roll (deg)') axs[2].set_xticklabels([]) axs[3].plot(ts, rpy[1], label='true') axs[3].plot(ts, estimated_rpy[1], '--', label='estimated') axs[3].grid(True) axs[3].legend(loc='upper right') axs[3].set_ylabel('pitch (deg)') axs[3].set_xticklabels([]) axs[4].plot(ts, rpy[2], label='true') axs[4].plot(ts, estimated_rpy[2], '--', label='estimated') axs[4].grid(True) axs[4].legend(loc='upper right') axs[4].set_ylabel('yaw (deg)') axs[4].set_xlabel('time (sec)') plt.show() def get_gyro_data(q1, q2, dt, noise): mean_x = 2/dt * (q1[0]*q2[1] - q1[1]*q2[0] - q1[2]*q2[3] + q1[3]*q2[2]) mean_y = 2/dt * (q1[0]*q2[2] + q1[1]*q2[3] - q1[2]*q2[0] - q1[3]*q2[1]) mean_z = 2/dt * (q1[0]*q2[3] - q1[1]*q2[2] + q1[2]*q2[1] - q1[3]*q2[0]) x = random_generator.normal(mean_x, noise) y = random_generator.normal(mean_y, noise) z = random_generator.normal(mean_z, noise) return x, y, z def get_accelerometer_data(q, noise): q_to_body = quaternion_inv(q) up_world = [0, 0, -g] up_body = rotate_vector(q_to_body, up_world) x = random_generator.normal(up_body[0], noise) y = random_generator.normal(up_body[1], noise) z = random_generator.normal(up_body[2], noise) return x, y, z def generate_accelerometer_data_array(q, acc_noise): N = len(q) ax, ay, az = [None] * N, [None] * N, [None] * N for i in range(N): ax[i], ay[i], az[i] = get_accelerometer_data(q[i], acc_noise) return ax, ay, az def generate_gyro_data_array(t, q, gyro_noise): N = len(t) wx, wy, wz = [None] * N, [None] * N, [None] * N for i in range(1, N): dt = t[i] - t[i-1] wx[i], wy[i], wz[i] = get_gyro_data(q[i-1], q[i], dt, gyro_noise) return wx, wy, wz def estimate(t, w, a): N = len(t) q = [None] * N ekf = EKF() for i in range(1, N): dt = t[i] - t[i-1] wi = [w[0][i], w[1][i], w[2][i]] ai = [a[0][i], a[1][i], a[2][i]] ekf.predict(wi, dt) ekf.update(ai) q[i] = ekf.x return q def quaternion_to_euler_degrees(q): N = len(q) roll = [None] * N pitch = [None] * N yaw = [None] * N for i in range(N): if q[i] is not None: r, p, y = quaternion_to_euler(q[i]) roll[i] = np.degrees(r) pitch[i] = np.degrees(p) yaw[i] = np.degrees(y) return roll, pitch, yaw # Fixed (non-rotating) at roll 25 degrees, pitch 0 degrees, yaw 0 degrees def generate_test1_data(t): N = len(t) roll = np.radians(25) pitch = np.radians(0) yaw = np.radians(0) q = [None] * N for i in range(N): q[i] = quaternion_from_euler(roll, pitch, yaw) return q # Rotating at constant angular rate [90 degrees/sec, 0, 0] def generate_test2_data(t): N = len(t) q = [None] * N q[0] = quaternion_identity() rate = 90 w = np.radians([rate, 0, 0]) abs_w = np.linalg.norm(w) for i in range(1, N): dt = t[i] - t[i-1] dtheta = abs_w * dt unit_axis = w / abs_w dq = quaternion_from_axis_angle(unit_axis, dtheta) q[i] = quaternion_multiply(q[i-1], dq) q[i] = normalize(q[i]) return q # Rotating all axes at the same time def generate_test3_data(t): N = len(t) q = [None] * N q[0] = quaternion_identity() wx = 500 * np.sin(2 * np.pi * 0.5 * t) wy = 200 * np.sin(2 * np.pi * 1.0 * t) wz = 300 * np.sin(2 * np.pi * 2.0 * t) for i in range(1, N): dt = t[i] - t[i-1] w = np.radians([wx[i], wy[i], wz[i]]) abs_w = np.linalg.norm(w) if abs_w > 0: dtheta = abs_w * dt unit_axis = w / abs_w dq = quaternion_from_axis_angle(unit_axis, dtheta) else: dq = quaternion_identity() dq = quaternion_from_axis_angle(unit_axis, dtheta) q[i] = quaternion_multiply(q[i-1], dq) q[i] = normalize(q[i]) return q GYRO_NOISE = 0.015 # rad/sec ACCELEROMETER_NOISE = 1.0 # m/s^2 # Generate time t0 = 0 tf = 5 dt = 0.01 t = np.arange(t0, tf, dt) # Generate test data #q = generate_test1_data(t) #q = generate_test2_data(t) q = generate_test3_data(t) # Generate sensor data a = generate_accelerometer_data_array(q, ACCELEROMETER_NOISE) w = generate_gyro_data_array(t, q, GYRO_NOISE) # EKF estimation estimated_q = estimate(t, w, a) # Check results rpy = quaternion_to_euler_degrees(q) estimated_rpy = quaternion_to_euler_degrees(estimated_q) plot(t, w, a, rpy, estimated_rpy)