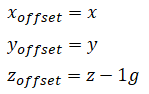
Accelerometer Calibration Methods

This is a summary of different methods to calibrate an accelerometer. Units are in G.

Method 1: One Point Calibration ^[1]

This method requires the device to be positioned in only one orientation. The device must be placed on a flat surface that is not tilted.

Calibration

Steps to compute calibration parameters

Place the accelerometer on a flat surface (Z up)
Record x, y, z
Calculate offset parameters:

Usage

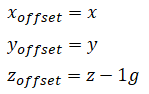
Method to compute calibrated values from raw measurements

Method 2: Full Range Calibration ^[2]

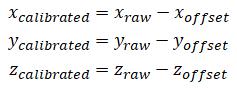
This method requires the device to be rotated to find its maximum and minimum values.

Calibration

Steps to compute calibration parameters

Rotate the device while z is up to find z's maximum value
Rotate the device while z is down to find z's minimum value
Repeat for x and y
You should now have 3x2=6 measurements
Calculate 6 calibration parameters:

Usage

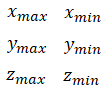
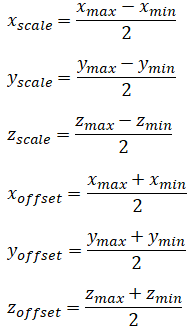
Method to compute calibrated values from raw measurements

Method 3: Six Point Calibration ^[1]

This method requires the device to be positioned in six different orientations. The device must have 6 perpendicular sides and be placed on a flat surface that is not tilted.

Model

The following calibration model is used:

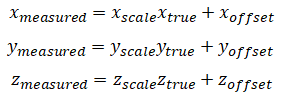
where x_measured y_measuredz_measured are the raw measured values from the accelerometer and x_true y_true z_true are the real acceleration experienced by the device (a.k.a calibrated values). x_scale y_scale z_scale x_offset y_offset z_offset are calibration parameters.

Calibration

Steps to compute calibration parameters

Place the accelerometer on a flat surface
Record x, y, z
Repeat for the other 5 faces
You should now have 3x6=18 measurements
Calculate 6 calibration parameters:

Usage

Method to compute calibrated values from raw measurements

Example (Python)

# Measurements for calibration
xup_x  , xup_y  , xup_z   =  1.2,  0.0,  0.1
xdown_x, xdown_y, xdown_z = -1.0,  0.0,  0.1
yup_x  , yup_y  , yup_z   =  0.1,  1.1,  0.1
ydown_x, ydown_y, ydown_z =  0.1, -1.1,  0.1
zup_x  , zup_y  , zup_z   =  0.1,  0.0,  1.1
zdown_x, zdown_y, zdown_z =  0.1,  0.0, -0.9

# Calibration parameters
offset_x = (yup_x + ydown_x + zup_x + zdown_x) / 4
offset_y = (xup_y + xdown_y + zup_y + zdown_y) / 4
offset_z = (xup_z + xdown_z + yup_z + ydown_z) / 4
scale_x = (xup_x - xdown_x) / 2
scale_y = (yup_y - ydown_y) / 2
scale_z = (zup_z - zdown_z) / 2

# Calibrated values
raw_x = xup_x
raw_y = xup_y
raw_z = xup_z
calibrated_x = (raw_x - offset_x) / scale_x
calibrated_y = (raw_y - offset_y) / scale_y
calibrated_z = (raw_z - offset_z) / scale_z
print(calibrated_x)
print(calibrated_y)
print(calibrated_z)

Output

0.9999999999999998
0.0
0.0

Method 4: Six Point Calibration 2 ^[3]

This method requires the device to be positioned in six different orientations. The device must have 6 perpendicular sides and be placed on a flat surface that is not tilted.

Model

The following calibration model is used:

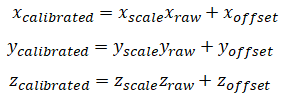
where x_raw y_raw z_raw are the raw measured values from the accelerometer and x_calibrated y_calibrated z_calibrated are the calibrated values. x_scale, y_scale, z_scale, x_offset y_offset z_offset are calibration parameters.

Calibration

Steps to compute calibration parameters

Place the accelerometer on a flat surface
Record x, y, z
Repeat for the other 5 faces
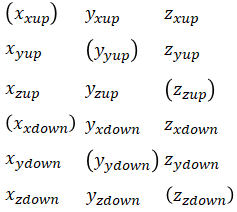You should now have 3x6=18 measurements Only the 6 measurements in brackets are used to calculate the parameters
Calculate 6 calibration parameters:

Usage

Method to compute calibrated values from raw measurements

Example (Python)

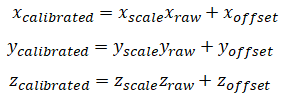
# Measurements for calibration
xup_x  , xup_y  , xup_z   =  1.2,  0.0,  0.1
xdown_x, xdown_y, xdown_z = -1.0,  0.0,  0.1
yup_x  , yup_y  , yup_z   =  0.1,  1.1,  0.1
ydown_x, ydown_y, ydown_z =  0.1, -1.1,  0.1
zup_x  , zup_y  , zup_z   =  0.1,  0.0,  1.1
zdown_x, zdown_y, zdown_z =  0.1,  0.0, -0.9

# Calibration parameters
offset_x = -(xup_x + xdown_x) / (xup_x - xdown_x)
offset_y = -(yup_y + ydown_y) / (yup_y - ydown_y)
offset_z = -(zup_z + zdown_z) / (zup_z - zdown_z)
scale_x = 2 / (xup_x - xdown_x)
scale_y = 2 / (yup_y - ydown_y)
scale_z = 2 / (zup_z - zdown_z)

# Calibrated values
raw_x = xup_x
raw_y = xup_y
raw_z = xup_z
calibrated_x = scale_x * raw_x + offset_x
calibrated_y = scale_y * raw_y + offset_y
calibrated_z = scale_z * raw_z + offset_z
print(calibrated_x)
print(calibrated_y)
print(calibrated_z)

Output

1.0
0.0
-2.7755575615628914e-17

Method 5: Six Point Calibration 3 ^[4]

This method requires the device to be positioned in six different orientations. The device must have 6 perpendicular sides and be placed on a flat surface that is not tilted.

Model

The following calibration model is used:

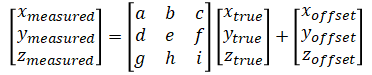
where [x_measured y_measured z_measured] is the raw measured values from the accelerometer and [x_true y_true z_true] is the real acceleration (a.k.a calibrated values). a~i and [x_offset y_offset z_offset] are calibration parameters.

Calibration

Steps to compute calibration parameters

Place the accelerometer on a flat surface
Record x, y, z
Repeat for the other 5 faces
You should now have 3x6=18 measurements
Calculate 12 calibration parameters:

Usage

Method to compute calibrated values from raw measurements

Example (Python)

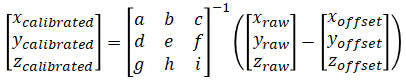
import numpy as np

# Measurements for calibration
xup_x  , xup_y  , xup_z   =  1.2,  0.0,  0.1
xdown_x, xdown_y, xdown_z = -1.0,  0.0,  0.1
yup_x  , yup_y  , yup_z   =  0.1,  1.1,  0.1
ydown_x, ydown_y, ydown_z =  0.1, -1.1,  0.1
zup_x  , zup_y  , zup_z   =  0.1,  0.0,  1.1
zdown_x, zdown_y, zdown_z =  0.1,  0.0, -0.9

# Calibration parameters
offset_x = (xup_x + xdown_x + yup_x + ydown_x + zup_x + zdown_x) / 6
offset_y = (xup_y + xdown_y + yup_y + ydown_y + zup_y + zdown_y) / 6
offset_z = (xup_z + xdown_z + yup_z + ydown_z + zup_z + zdown_z) / 6
a = ((xup_x - offset_x) + (-xdown_x + offset_x)) / 2
b = ((yup_x - offset_x) + (-ydown_x + offset_x)) / 2
c = ((zup_x - offset_x) + (-zdown_x + offset_x)) / 2
d = ((xup_y - offset_y) + (-xdown_y + offset_y)) / 2
e = ((yup_y - offset_y) + (-ydown_y + offset_y)) / 2
f = ((zup_y - offset_y) + (-zdown_y + offset_y)) / 2
g = ((xup_z - offset_z) + (-xdown_z + offset_z)) / 2
h = ((yup_z - offset_z) + (-ydown_z + offset_z)) / 2
i = ((zup_z - offset_z) + (-zdown_z + offset_z)) / 2

# Calibrate raw values

A = np.array([
    [a, b, c],
    [d, e, f],
    [g, h, i]
])

raw = np.array([
    [xup_x],
    [xup_y],
    [xup_z]
])

offset = np.array([
    [offset_x], 
    [offset_y], 
    [offset_z]
])

calibrated = np.linalg.inv(A) @ (raw - offset)

print(calibrated)

Output

[[1.00000000e+00]
[0.00000000e+00]
[1.38777878e-17]]

Method 6: N Point Calibration ^[4][5]

This method requires the device to be positioned in any number of orientations. For each orientation, a true acceleration must be known.

Model

The following calibration model is used:

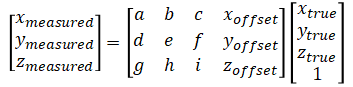
where [x_measured y_measured z_measured] is the raw measured values from the accelerometer and [x_true y_true z_true] is the real acceleration (a.k.a calibrated values). a~i and x_offset y_offset z_offset are calibration parameters.

Calibration

Steps to compute calibration parameters

Place the accelerometer in a certain orientation with known true acceleration
Record x, y, z
Repeat with N other orientations
You should now have 3xN measurements along with their true values
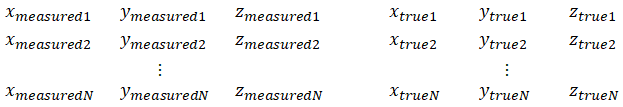
Calculate 12 calibration parameters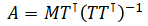: where A is 3x4 matrix (calibration parameters)

Usage

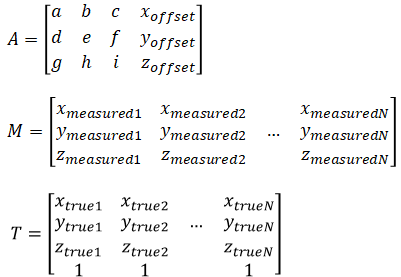
Method to compute calibrated values from raw measurements

Example (Python)

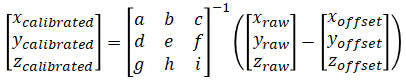
import numpy as np

# Measurements for calibration
xup_x  , xup_y  , xup_z   =  1.2,  0.0,  0.1
xdown_x, xdown_y, xdown_z = -1.0,  0.0,  0.1
yup_x  , yup_y  , yup_z   =  0.1,  1.1,  0.1
ydown_x, ydown_y, ydown_z =  0.1, -1.1,  0.1
zup_x  , zup_y  , zup_z   =  0.1,  0.0,  1.1
zdown_x, zdown_y, zdown_z =  0.1,  0.0, -0.9

measured = np.array([
    [xup_x, xdown_x, yup_x, ydown_x, zup_x, zdown_x],
    [xup_y, xdown_y, yup_y, ydown_y, zup_y, zdown_y],
    [xup_z, xdown_z, yup_z, ydown_z, zup_z, zdown_z]
])

true = np.array([
    [1, -1, 0,  0, 0,  0], 
    [0,  0, 1, -1, 0,  0], 
    [0,  0, 0,  0, 1, -1],
    [1,  1, 1,  1, 1,  1]
])

A = measured @ true.T @ np.linalg.inv(true @ true.T)

# Calibrate raw values
raw = np.array([
    [xup_x],
    [xup_y],
    [xup_z]
])

calibrated = np.linalg.inv(A[:,:3]) @ (raw - A[:,3:4])
print(calibrated)

Output

[[1.00000000e+00]
 [0.00000000e+00]
 [1.38777878e-17]]

Method 7: N Point Calibration 2 ^[3][6]

This method requires the device to be positioned in any number of orientations. For each orientation, a true acceleration must be known.

Model

The following calibration model is used:

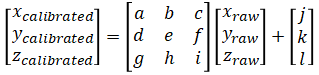
which can be rewritten as

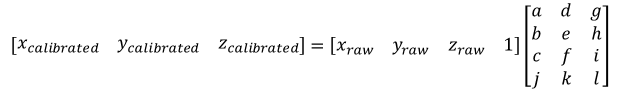
where [x_calibrated y_calibrated z_calibrated] is the calibrated values and [x_raw y_raw z_raw] is the raw accelerometer measurements. a~l are calibration parameters.

Calibration

Steps to compute calibration parameters

Place the accelerometer in a certain orientation with known true acceleration
Record x, y, z
Repeat with N other orientations
You should now have 3xN measurements along with their true values
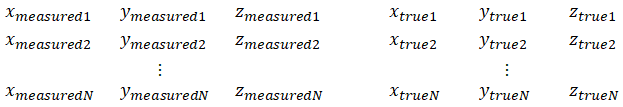
Calculate 12 calibration parameters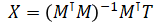: where X is 4x3 matrix (calibration parameters)

Usage

Method to compute calibrated values from raw measurements

Example (Python)

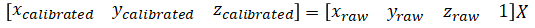
import numpy as np

# Measurements for calibration
xup_x  , xup_y  , xup_z   =  1.2,  0.0,  0.1
xdown_x, xdown_y, xdown_z = -1.0,  0.0,  0.1
yup_x  , yup_y  , yup_z   =  0.1,  1.1,  0.1
ydown_x, ydown_y, ydown_z =  0.1, -1.1,  0.1
zup_x  , zup_y  , zup_z   =  0.1,  0.0,  1.1
zdown_x, zdown_y, zdown_z =  0.1,  0.0, -0.9

measured = np.array([
    [xup_x  , xup_y  , xup_z  , 1],
    [xdown_x, xdown_y, xdown_z, 1],
    [yup_x  , yup_y  , yup_z  , 1],
    [ydown_x, ydown_y, ydown_z, 1],
    [zup_x  , zup_y  , zup_z  , 1],
    [zdown_x, zdown_y, zdown_z, 1]
])

true = np.array([
    [ 1,  0,  0],
    [-1,  0,  0],
    [ 0,  1,  0],
    [ 0, -1,  0],
    [ 0,  0,  1],
    [ 0,  0, -1]
])

X = np.linalg.inv(measured.T @ measured) @ measured.T @ true

# Calibrate raw values
raw = np.array([
    [xup_x, xup_y, xup_z, 1]
])

calibrated = raw @ X

print(calibrated)

Output

[[ 1.00000000e+00  0.00000000e+00 -1.38777878e-17]]

References

[1] Offset Calibration of the MMA8450Q (NXP AN3916/AN4069)
[2] Implementing Auto-Zero Calibration Technique for Accelerometers (NXP AN3447)
[3] High-Precision Calibration of a Three-Axis Accelerometer (NXP AN4399)
[4] 6-point tumble sensor calibration (ST DT0053 Design tip)
[5] LaValle "Virtual Reality", Cambridge University Press, 2023
[6] Parameters and calibration of a low-g 3-axis accelerometer (ST AN4508)

Accelerometer Calibration Methods

Method 1: One Point Calibration [1]

Calibration

Usage

Method 2: Full Range Calibration [2]

Calibration

Usage

Method 3: Six Point Calibration [1]

Model

Calibration

Usage

Example (Python)

Method 4: Six Point Calibration 2 [3]

Model

Calibration

Usage

Method 5: Six Point Calibration 3 [4]

Model

Calibration

Usage

Example (Python)

Output

Method 6: N Point Calibration [4][5]

Model

Calibration

Usage

Example (Python)

Method 7: N Point Calibration 2 [3][6]

Model

Calibration

Usage

Example (Python)

References

Method 1: One Point Calibration ^[1]

Method 2: Full Range Calibration ^[2]

Method 3: Six Point Calibration ^[1]

Method 4: Six Point Calibration 2 ^[3]

Method 5: Six Point Calibration 3 ^[4]

Method 6: N Point Calibration ^[4][5]

Method 7: N Point Calibration 2 ^[3][6]