Below are steps to design a controller for a system. An example is also provided.
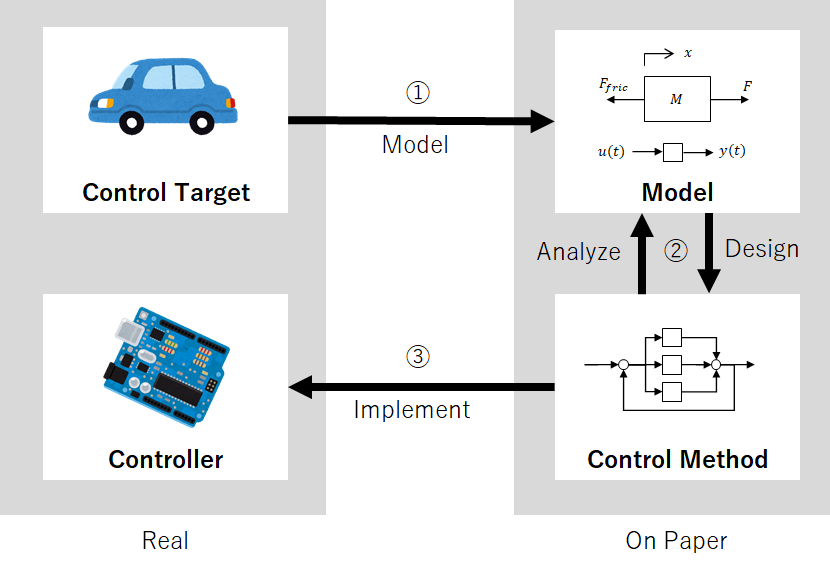 1. Modelling
1. Modelling
Create a model. Express the real system on paper. The model should:
Study the characteristics of the control target using the model. Then, design a control method.
Write code according to the previously determined control method.
A car moves along a line. Design a controller that moves the car to y = 0
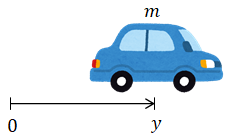 1. Modelling
1. Modelling
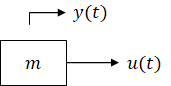
From Newton's second law:
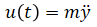 2. Design & Analysis
2. Design & Analysis
Control the force by using the car's position and velocity as feedback (as an example):
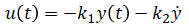
Substitute into the model and solve for the position, y(t) because we want y = 0:
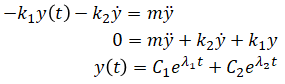
Where C1 and C2 depends on y(0) and ẏ(0) so we leave them.
λ1 and λ2 are:
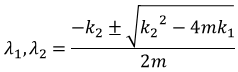
The objective is y = 0 so we want,
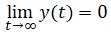
So we want λ1, λ2 < 0
So choose k1, k2 > 0
3. ImplementationC code:
loop()
{
y = get_position();
vy = get_velocity();
u = -k1 * y - k2 * vy;
set_force(u);
}
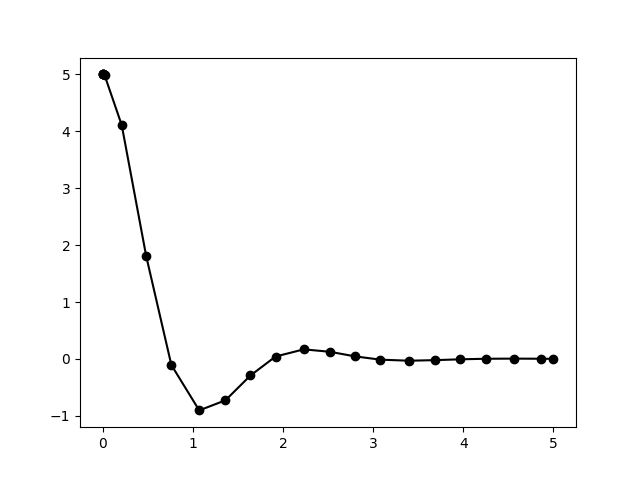
Simulation:
from scipy.integrate import solve_ivp import matplotlib.pyplot as plt # Constants m = 1 # Mass (kg) k1 = 10 k2 = 3 # dx/dt = f(t, x) # # t : Current time (seconds), scalar # x : Current state, [y, vy] # return: First derivative of state, [vy, ay] def xdot(t, x): # Controller (input, u) u = -k1 * x[0] - k2 * x[1] # Dynamics (dx/dt = xdot = [vz, az]) return [x[1], u/m] x0 = [5, 0] # Initial state, [y0, vy0] t_span = [0, 5] # Simulation time (seconds), [from, to] # Solve for the states, x(t) = [y(t), vy(t)] sol = solve_ivp(xdot, t_span, x0) # Plot z vs t plt.plot(sol.t, sol.y[0], 'k-o') plt.show()