PID Control

PID control is a feedback method used to control systems. Its benefits, mathematical form, and effects of each term are discussed below.

Benefits

Past, Current, and Future
PID control considers past, current, and the future behavior of the system.
- Proportional control (P) removes the current error.
- Integral control (I) removes the offset (past error).
- Derivative control (D) tries to predict how the system behaves in the future.
Logical Reasoning
Since PID is a linear controller, its behavior can be explained and analyzed logically. For example, it is possible to explain the effects of changing PID parameters. It is also possible to analyze whether the system stays stable when its characteristics change. These are difficult with counterparts such as fuzzy control and neural network.
Intuitive
The effects of each PID parameter can be explained qualitatively.
On-site Tuning
PID controller can be fine-tuned on-site. It is usually difficult to make a model that perfectly matches the actual process. Having the ability to adjust the controller after deployment is an important factor to consider.

Mathematical Form

Standard form:

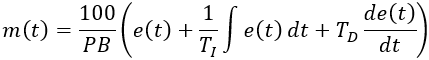
m(t)	Control output
e(t)	Error e(t) = SV(t) - PV(t) SV(t): target value PV(t): measured value
PB	Proportional band (%)
T_I	Integral time
T_D	Derivative time

Laplace form:

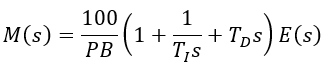
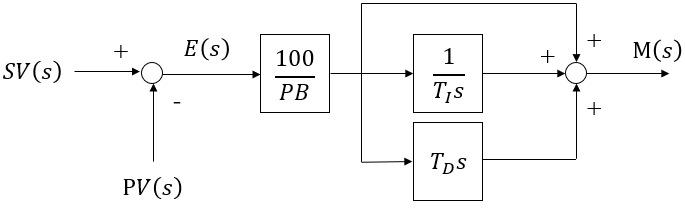
Block diagram:

Proportional Term

Proportional-only controller:

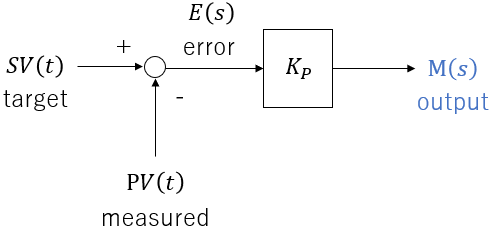
If there is a constant error c, the proportional controller keeps outputting a value proportional to that error.

Integral Term

Intagral-only controller:.

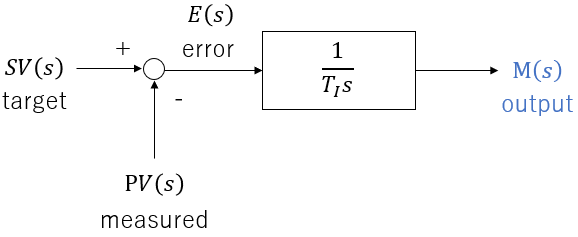
If there is a constant error c, the integrator controller outputs a value that increases over time. The rate at which the output increases is proportional to the error:

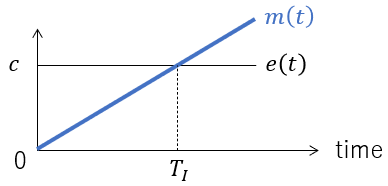
Output as a function of time:

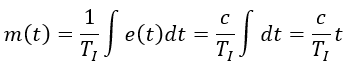
m(T_I) = c so T_I can be interpreted as the time it takes for the integrator output to reach c.

Integrator strength increases as T_I becomes smaller.

Derivative Term

Derivative-only controller:

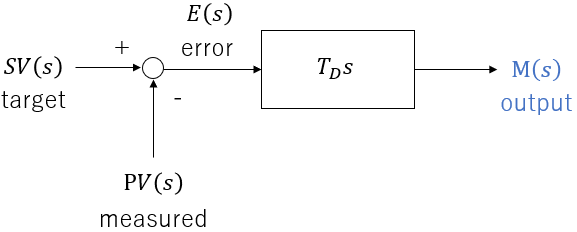
If there is a constant error that increases at a constant rate c, then the controller outputs a value that is proportional to this rate:

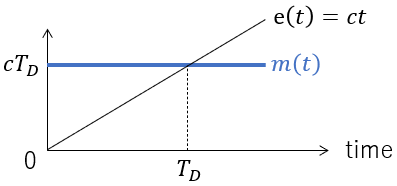
Output as a function of time:

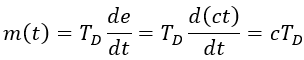
e(T_D) = cT_D can be interpreted as the time it takes for the error to match the derivative controller output (assuming an error that increases at a constant rate).

Derivative strength increases as T_D becomes larger.