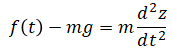
PD controller is developed to control a quadrotor in 1-dimensional space (height direction only).
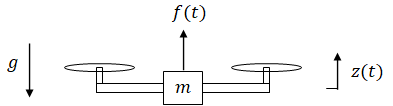
| (input) | f(t) | = | motor thrust | |
| (output) | z(t) | = | height | unknown |
| m | = | mass | ||
| g | = | gravitational acceleration |
1 unknown so 1 equation is needed.
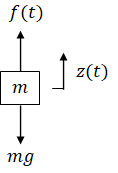
Newton's 2nd law:
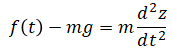
States:

Position and velocity are chosen as state variables because,
State vector:
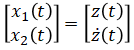
Input vector:
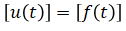
Output vector:
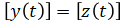
Rewrite (eq. 1) in these new notations:
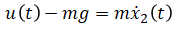
Rearrange equations to express ẋ(t) and y(t) in terms of x(t) and u(t):
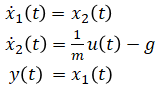
Rewrite as matrix:
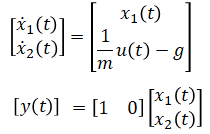
The objective is to design a controller (find the input thrust function) which makes the quadrotor track a trajectory (position, velocity, and acceleration as a function of time).

PD controller can be written as,
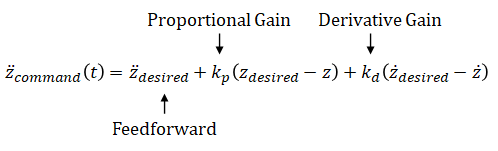
(eq. 1) can be solved for f(t)
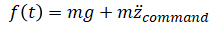
Substitute the PD controller:

Python code simulation. Quadrotor climbs to 1m height.
from scipy.integrate import solve_ivp import matplotlib.pyplot as plt # Constants g = 9.81 # Gravitational acceleration (m/s^2) m = 0.18 # Mass (kg) # dx/dt = f(t, x) # # t : Current time (seconds), scalar # x : Current state, [z, vz] # return: First derivative of state, [vz, az] def xdot(t, x): # Desired z, vz, az z_des = 1 vz_des = 0 az_des = 0 # PD Controller (input, u) kp = 30 kv = 3 u = m * (az_des + kp * (z_des - x[0]) + kv * (vz_des - x[1]) + g) # Clamp to actuator limits (0 to 2.12N) u = min(max(0, u), 2.12) # Quadrotor dynamics (dx/dt = xdot = [vz, az]) return [x[1], u/m - g] x0 = [0, 0] # Initial state, [z0, vz0] t_span = [0, 5] # Simulation time (seconds), [from, to] # Solve for the states, x(t) = [z(t), vz(t)] sol = solve_ivp(xdot, t_span, x0) # Plot z vs t plt.plot(sol.t, sol.y[0], 'k-o') plt.show()
Result:
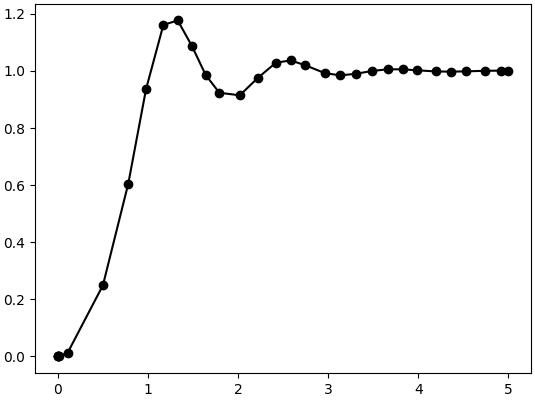
Note 1: PID is better when there are disturbances (like wind) and modeling errors (unknown mass) because it makes steady-state error go to zero. In such case, the closed loop system becomes third-order.
Note 2: information on this page is based off of an example in an online course[1]. It is modified and extended with additional information.
[1] Coursera, Robotics: Aerial Robotics