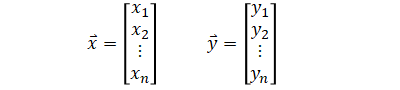
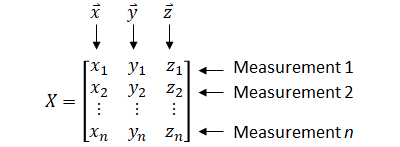
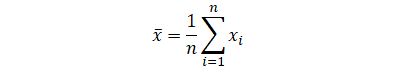
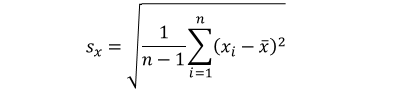
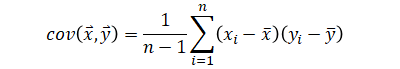
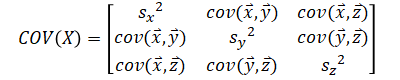

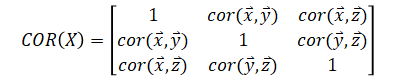
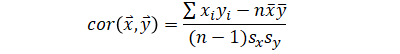
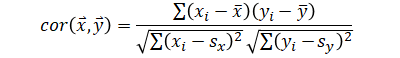

This page summarizes covariance and correlation formulas in both scalar and matrix forms. Formulas to convert between the two are provided as well.
Note: correlation refers to Pearson correlation coefficient which is what most people refer to when talking about correlation and this is also the default in many softwares.
Covariance (scalar) is a number calculated from two variables (two vectors of same length). The same is true with correlation.
Covariance matrix of an Nxp matrix is a pxp matrix. Same is true with correlation matrix.
| Scalar | Matrix | |
|---|---|---|
| Input | 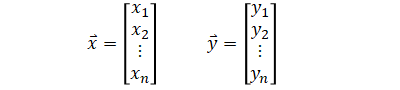 |
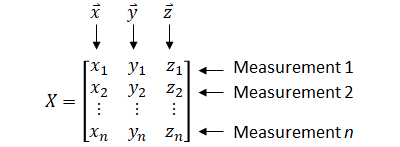 |
| Mean | 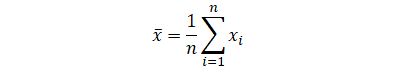 |
- |
| Standard Deviation | 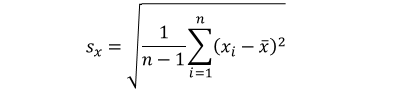 |
- |
| Covariance | 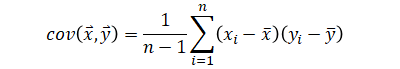 |
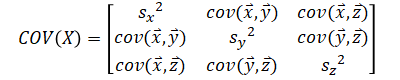 |
| Correlation |  |
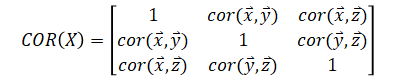 |
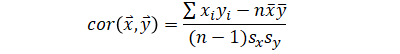 |
||
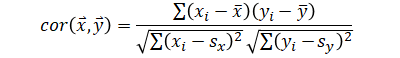 |
||
 |
| Scalar | Matrix | |
|---|---|---|
| Correlation to covariance | 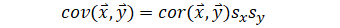 |
 |
| Covariance to correlation | 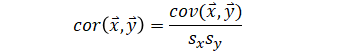 |
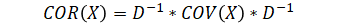 |
| Correlation using covariance | 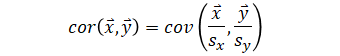 |
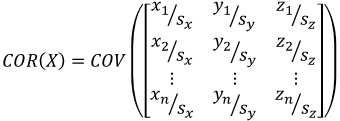 |
- "*" is matrix multiplication.
- Matrix multiplication is associative: (AB)C = A(BC)
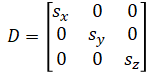
Standard deviation and covariance are different for sample and population:
| Sample | Population | |
|---|---|---|
| Standard Deviation | 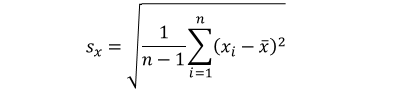 |
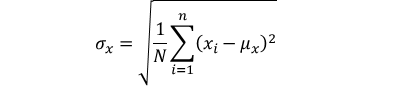 |
| Covariance |  |
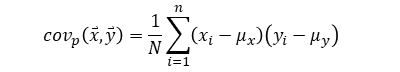 |
| Mean | 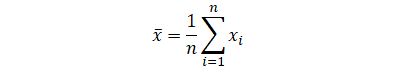 |
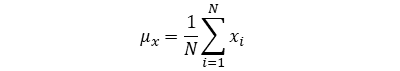 |
N = population size
n = sample size (n < N)
On the other hand, correlation value is the same for sample and population because their difference cancels out. When calculating correlation with any of the formulas with standard deviation in it, correlation formula will be different so the appropriate one should be used to yield the correct value:
| Using sx, sy | Using σx, σy | |
|---|---|---|
| Correlation |  |
 |
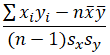 |
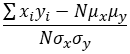 |
Similarly during conversion, if correlation is calculated by dividing standard deviation from population covariance, standard deviation has to be calculated with 1/N. If covariance is calculated by multiplying standard deviation with correlation, the result is population covariance if population standard deviation was used. The mean is always 1/n and not 1/(n-1).
Sample is usually the default in software tools:
| Excel | R | MATLAB | ||
|---|---|---|---|---|
| Standard Deviation | Sample | STDEV.S() |
sd() |
std() |
| Population | STDEV.P() |
- | std(__,w=1) |
|
| Covariance | Sample | COVARIANCE.S() |
cov() |
cov() |
| Population | COVARIANCE.P() |
- | cov(__,w=1) |
|
| Correlation | CORREL() |
cor() |
corrcoef() |
|
The difference is small but important because, for example, if you did not know this, you would not be able to debug (check) if a system that uses these statistical methods is coded correctly.
If there is freedom to choose between sample or population standard deviation (or covariance), use population formula when quantifying variation of provided data only (e.g. standard deviation of exam scores). Use sample formula when estimating variation of overall population by analyzing a sample of that data. (e.g. standard deviation of heights of all humans on Earth calculated from 100 randomly selected people's heights) The latter is more common because you are usually trying to extrapolate and draw wider conclusions about the general population using a sample of that population.